الهيدروديناميكيّة المغناطيسيّة أو " Magnetohydrodynamics".

 

هيدرو-ديناميكا مغناطيسية

من ويكيبيديا، الموسوعة الحرة

هيدروديناميكا مغناطيسية

صنف فرعي من

ميكانيكا الموائع عدل القيمة على Wikidata

جزء من

hydrodynamics (en) ترجم عدل القيمة على 

 Wikidata

الشمس هي محطة توليد هيدروديناميكية مغناطيسية لم تُدرس بشكل جيد حتّى الآن 

علم الهيدروديناميكية المغناطيسيّة ويسمى أيضاً (علم ديناميكية أوهيدروليكية السوائل المغناطيسية) هو العلم الذي يدرس الخصائص المغناطيسية وسلوك الموائع الموصلة كهربائيّاً. ومن أمثلة الموائع المغناطيسية (البلازما، المعادن السائلة، المياه الملحية، المحاليل الكهربائيّة والإلكتروليتات).

 

كلمة الهيدروديناميكيّة المغناطيسيّة أو " Magnetohydrodynamics" مشتقة من (Magneto) وتعني الحقل المغناطيسي، (Hydro) وتعني المياه، و (Dynamic)وتعني الحركة. 

= علم الهيدروديناميكية المغناطيسيّة أو ما يعرف اختصاراً بـ (MHD) أُسِّسَ على يد العالم السويدي هانز ألفين الذي حصل على جائزة نوبل في الفيزياء في عام 1970 وذلك لتأسيسه لهذا العلم.

 

المفهوم الأساسي للـ MHD هو أنّ المجالات المغناطيسية يمكن أن تحفّز التيارات في المائع المتحرك الذي يحمل خاصية الموصليّة الكهربائية، مما يؤدّي لاستقطاب المائع وتغيير المجال المغناطيسي له بالتبادل. إنّ مجموعة المعادلات التي تصف (MHD) هي مزيج من معادلات نافييه-ستوكس لديناميكا الموائع ومعادلات ماكسويل للكهرومغناطيسية. يجب حل هذه المعادلات التفاضلية المترابطة، إما تحليليًا أو عدديًا.

محتويات

 

1 تاريخ الـ (الهيدروديناكيكية المغناطيسية)

2 الهيدروديناكيكية المغناطيسية المثالية والمقاومة

2.1 معادلات MHD المثالية

2.2 قابلية تطبيق الـ MHD المثالي على البلازما

2.3 أهمية المقاومة

2.4 أهمية التأثيرات الحركية

3 البنية في أنظمة الهيدروديناكيكية المغناطيسية

4 اقرأ أيضا

5 المصادر

 

تاريخ الـ (الهيدروديناكيكية المغناطيسية)

أول استخدام مسجل لمصطلح (الهيدروديناكيكية المغناطيسية) تمّ من قبل العالم والمهندس الكهربائي السويدي هانز ألففين عام 1942 عندما قال: «أخيرًا، بعض الملاحظات حول نقل النشاط من الشمس إلى الكواكب، وهو أمر أساسي للنظرية (§11). وأشير إلى أهمية الموجات الهدروديناميكية المغناطيسية في هذا الصدد.»المياه المالحة المنحسرة المتدفقة عبر جسر ووترلو في لندن تتفاعل مع الحقل المغناطيسي الأرضي مخلّفة فرق في الكمون ما بين ضفتي النهر. وصف مايكل فاراداي هذا التأثير بأنه «تحريض كهرطيسي» وقام بهذه التجربة عام 1832 لكن التيار الذي نتج عنها كان صغيراً جدّاً بحيث لا يمكن قياسه بالمعدّات الموجودة في ذلك الزمن، وقد ساهم قاع النهر في قصر الإشارة الكهربائية الناتجة. ومع ذلك، فقد تمّ قياس الجهد الناجم عن حركات المد والجزر في القنال الإنجليزي عام 1851من خلال عملية مشابهة.

الهيدروديناكيكية المغناطيسية المثالية والمقاومة

 

إنّ أبسط أشكال الهيدروديناميكية المغناطيسة هي الهيدروديناميكية المغناطيسية المثالية (Ideal MHD)، يُفترض في هذه الحالة أنّ السائل لديه مقاومة قليلة جدّاً لدرجة أنه يمكن التعامل معه على أنّه موصل مثالي. وهذه الحالة نكون عند الحد الأعلى لعدد رينولد المغناطيسي.

 

في الـ MHD المثالي، يَفرِضُ قانون لينز أنّ السائل مرتبط إلى حدٍّ ما بخطوط المجال المغناطيسي. للتوضيح، فإنّ في حالة الـ MHD المثالي، يأخذ حجمٌ صغيرٌ من السوائل شكل حبل يحيط بخط الحقل ويتوضع على طول خط المجال المغناطيسي، حتّى عندما يكون ملتويًا ومشوَّهًا بتدفّقات السوائل في النظام. ويشار إلى ذلك أحياناً باسم)خطوط المجال المغناطيسي «المجمدة» في السائل). [5] العلاقة بين خطوط الحقل المغنطيسي والسوائل في الـ MHD المثالي تعمل على إصلاح طوبولوجيا المجال المغناطيسي في السائل - على سبيل المثال، إذا رُبطت مجموعة من خطوط المجال المغناطيسي لتُشَكّل عقدة، فستبقى هكذا طالما أن السائل أو البلازما لديه مقاومة قليلة جدّاً لدرجة يمكن إهمالها. هذه الصعوبة في إعادة ربط خطوط الحقل المغناطيسي تجعل من الممكن تخزين الطاقة عن طريق تحريك السائل أو مصدر المجال المغناطيسي. ومن الممكن أن تصبح الطاقة متاحة إذا لم تعد حالة الـ MHD مثالية، مما يسمح بإعادة الاتصال المغناطيسي وهو ما يحرر الطاقة المخزنة من المجال المغناطيسي.

معادلات MHD المثالية

 

تتكون معادلات الـ MHD المثالية من: معادلة الاستمرارية، معادلة كوشي للقوّة الدافعة، قانون أمبير مع إهمال تيّار الإزاحة، ومعادلة تطور الحرارة. كما هو الحال مع أيّ وصف لأيّ سائل بأي نظام ناشط، يجب تطبيق مقاربة الإغلاق عند أعلى عزم في معادلة توزيع الجسيمات. يتم تحقيق هذا في أغلب الأحيان بالتقريب إلى تدفق الحرارة بعملية إيزوثيرميّة (أي بثبات درجة الحرارة) أو بعملية أديباتيّة (أي في بيئة معزولة عن الوسط الخارجي بحيث لا يحدث تبادل حراري بين الوسط الذي تحدث فيه العملية والوسط الخارجي)

 

إن المعايير الرئيسية التي تميّز السائل الموصل كهربائياً هي: حقل سرعة البلازما السائلة v ، وكثافة التيار J ، والكثافة الكلية ρ، وضغط البلازما p. إنّ الشحنة الكهربائية المتدفّقة في البلازما هي مصدر المجال المغناطيسي B والحقل الكهربائي E. بشكل عامّ فإن جميع المعايير السابقة تتفاوت مع الزمن t. يُستخدم عادةً رمز المتّجه في هذه المعادلات، بالتفصيل: (الرمز ودلالته): ∇: يرمز للتدرج، ∇⋅: يرمز للتباعد، و ∇ ×: يرمز للتموج.

 

معادلة استمرارية الكتلة هي:

 

∂ ρ ∂ t + ∇ ⋅ ( ρ v ) = 0. {\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \left(\rho \mathbf {v} \right)=0.} {\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \left(\rho \mathbf {v} \right)=0.}

 

معادلة كوشي للقوّة الدافعة هي:

 

ρ ( ∂ ∂ t + v ⋅ ∇ ) v = J × B − ∇ p . {\displaystyle \rho \left({\frac {\partial }{\partial t}}+\mathbf {v} \cdot \nabla \right)\mathbf {v} =\mathbf {J} \times \mathbf {B} -\nabla p.} {\displaystyle \rho \left({\frac {\partial }{\partial t}}+\mathbf {v} \cdot \nabla \right)\mathbf {v} =\mathbf {J} \times \mathbf {B} -\nabla p.}

 

يمكن توسيع مصطلح قوة لورينتز J × B باستخدام قانون أمبير والمحددات الخاصة بمتجه الحركة

 

1 2 ∇ ( B ⋅ B ) = ( B ⋅ ∇ ) B + B × ( ∇ × B ) {\displaystyle {\frac {1}{2}}\nabla (\mathbf {B} \cdot \mathbf {B} )=(\mathbf {B} \cdot \nabla )\mathbf {B} +\mathbf {B} \times (\nabla \times \mathbf {B} )} {\displaystyle {\frac {1}{2}}\nabla (\mathbf {B} \cdot \mathbf {B} )=(\mathbf {B} \cdot \nabla )\mathbf {B} +\mathbf {B} \times (\nabla \times \mathbf {B} )}

 

ما يعطي:

 

J × B = ( B ⋅ ∇ ) B μ 0 − ∇ ( B 2 2 μ 0 ) , {\displaystyle \mathbf {J} \times \mathbf {B} ={\frac {\left(\mathbf {B} \cdot \nabla \right)\mathbf {B} }{\mu _{0}}}-\nabla \left({\frac {B^{2}}{2\mu _{0}}}\right),} {\displaystyle \mathbf {J} \times \mathbf {B} ={\frac {\left(\mathbf {B} \cdot \nabla \right)\mathbf {B} }{\mu _{0}}}-\nabla \left({\frac {B^{2}}{2\mu _{0}}}\right),}

 

حيث: الطرف الأوّل هو قوّة الشد المغناطيسي والطرف الثاني يمثّل قوّة الضغط المغناطيسيّة ويتمّ إعطاء قانون أوم المثالي للبلازما بالشكل التالي:

 

E + v × B = 0. {\displaystyle \mathbf {E} +\mathbf {v} \times \mathbf {B} =0.} {\displaystyle \mathbf {E} +\mathbf {v} \times \mathbf {B} =0.}

 

وقانون فاراداي هو:

 

∂ B ∂ t = − ∇ × E . {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=-\nabla \times \mathbf {E} .} {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=-\nabla \times \mathbf {E} .}

 

يهمل قانون أمبير منخفض التردّد تيار الإزاحة ويعطى بالعلاقة:

 

μ 0 J = ∇ × B . {\displaystyle \mu _{0}\mathbf {J} =\nabla \times \mathbf {B} .} {\displaystyle \mu _{0}\mathbf {J} =\nabla \times \mathbf {B} .}

 

علاقة التباعد المغناطيسي الكابح هي:

 

∇ ⋅ B = 0. {\displaystyle \nabla \cdot \mathbf {B} =0.} {\displaystyle \nabla \cdot \mathbf {B} =0.}

 

ومعادلة الطاقة تكون بالشكل التالي:

 

d d t ( p ρ γ ) = 0 , {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {p}{\rho ^{\gamma }}}\right)=0,} {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {p}{\rho ^{\gamma }}}\right)=0,}

 

حيث γ = 5/3 هي نسبة درجات الحرارة المعيّنة لمعادلة ثابت الحرارة للحالة. هذه المعادلة للطاقة ولا تطبّق إلّا في حالة انعدام وجود صدمات أو توصيل للحرارة، حيث أنّ المعادلة تفترض أن الإنتروبيا لعنصر مائع لا يتغير.

قابلية تطبيق الـ MHD المثالي على البلازما

 

لا ينطبق MHD المثالي إلا عندما:

 

تكون البلازما شديدة الصلابة بحيث يكون المقياس الزمني للتّصادمات أقصر من الأوقات المميًزة الأخرى في النظام، وبالتالي يكون توزيع الجسيمات قريب من توزيع (ماكسويل).

أن تكون المقاومة صغيرة بسبب هذه الاصطدامات. على وجه الخصوص، يجب أن تكون أوقات الانتشار للمغناطيسية النموذجية على طول أي مقياس موجود في النظام أطول من أي مقياس زمني.

الاهتمام بمقاييس الطول أطول بكثير من عمق القشرة الأيونيّة ونصف قطر لارمور المتعامد مع الحقل، طويل على كل مسافة الحقل بشكل يكفي لإهمال تخميد لانداو، وقياس الوقت أطول بكثير من زمن الدوران الأيوني (النظام سلس ومتطور ببطء).

 

أهمية المقاومة

 

في السائل الموصِل بشكل غير كامل، يمكن للحقل المغنطيسي أن يتحرّك خلال السائل تبعاً لقانون الانتشار وذلك مع مقاومة البلازما التي تكون بمثابة ثابت للانتشار. وهذا يعني أن حلول معادلات MHD المثالية لا تنطبق إلّا على فترة زمنية محدودة لمنطقة ذات حجم معين معطى قبل أن يصبح الانتشار كبيراً للغاية بحيث لا يمكن تجاهله. يمكن تقدير زمن الانتشار عبر منطقة نشطة بالطاقة الشمسية (من مقاومة الاصطدام) من مئات إلى آلاف السنين، أطول بكثير من العمر الفعلي للبقعة الشمسية، لذا يبدو من المعقول تجاهل المقاومة. وعلى النقيض من ذلك، فإن متر مكعب من مياه البحر يحتوي على زمن انتشار مغناطيسي يقاس بالمللي ثانية.

 

حتى في الأنظمة الفيزيائية - الكبيرة والموصلة بدرجة كافية، بحيث تقترح التقديرات البسيطة لرقم لاندكويست إلى أنه يمكن تجاهل المقاومة - قد تظل المقاومة مهمّة: العديد من حالات عدم الاستقرار يمكن أن تزيد من المقاومة الفعّالة للبلازما من خلال عدة عوامل ما يزيد عن مليار مرّة. تتكوّن المقاومة المعزّزة عادة نتيجة لتشكيل بنية صغيرة الحجم مثل تيار الصفائح أو الاضطراب المغناطيسي الرقيق النطاق، بإدخال مقاييس مكانية صغيرة في النظام الذي يتم فيه كسر الـ MHD المثاليّ يمكن أن يحدث الانتشار المغناطيسي بسرعة. عند حدوث ذلك، قد يحدث إعادة اتصال مغناطيسي في البلازما لتحرير الطاقة المغناطيسية المخزنة كموجات، وتسارع ميكانيكي كبير للمواد، وتسارع الجسيمات، والحرارة.

 

إنّ إعادة الربط المغنطيسي في الأنظمة عالية التوصيل أمر مهم لأنّه يركز الطاقة في الزمان والمكان، بحيث يمكن للقوى الصغيرة المطبّقة على البلازما لفترات طويلة من الزمن أن تتسبّب في حدوث انفجارات عنيفة وانبعاثات إشعاعيّة.

 

عندما لا يمكن اعتبار السوائل موصلة بالكامل، مع تحقّق الشروط الأخرى للـ MHD المثالي بشكل مرضٍ، فمن الممكن استخدام نموذج موسّع يسمى (MHD مقاوم). وهذا يشمل مصطلح إضافي في قانون أوم الذي يميّز المقاومة الاصطلاحية. بشكل عام، تكون المحاكاة الحاسوبية لـ MHD مقاومة بعض الشيء، نظرًا لأن شبكتها الحاسوبية تُدخل مقاومة رقمية.

أهمية التأثيرات الحركية

 

هناك قيد آخر لـ MHD (ونظريات السوائل بشكل عام) هو أنّها تعتمد على افتراض أن البلازما هي شديدة الاصطدام (وهذا هو المعيار الأول المذكور أعلاه)، بحيث يكون المقياس الزمني للتصادمات أقصر من الأوقات المميزة الأخرى في النظام، وتوزيعات الجسيمات تكون بطريقة ماكسويل. وهذا ليس هو الحال عادة في البلازما الاندماجية والفضائية والفيزياء الفلكية. وعندما لا يكون هذا هو الحال، أو عندما تكون الدراسة في المقاييس المكانية الأصغر، قد يكون من الضروري استخدام نموذج حركي يقوم بالحسابات لعامل التوزيع للشكل غير الماكسويلي بشكل صحيح. ومع ذلك، نظرًا لأن MHD بسيط نسبيًا ويلتقط العديد من الخصائص المهمة لديناميكيات البلازما، فغالبًا ما يكون دقيقًا بشكلٍ نوعيّ، ولذلك غالبًا ما يكون النموذج الأول للتجارب.

 

التأثيرات الحركية بشكل أساسي والتي لا يتم التقاطها بواسطة النماذج السائلة تشمل تشكّل طبقات مزدوجة، تخميد لانداو، مجموعة واسعة غير مستقرة، الفصل الكيميائي في البلازما الفضائية والإلكترون الجامح. في حالة تفاعلات الليزر فائقة الكثافة، تعني الجداول الزمنية القصيرة للغاية لترسب الطاقة أن الرموز الهيدروديناميكية تفشل في تفسير الفيزياء الأساسية.

البنية في أنظمة الهيدروديناكيكية المغناطيسية

 

في العديد من أنظمة MHD ، يتم ضغط معظم التيار الكهربائي إلى أشرطة رقيقة شبه ثنائية الأبعاد تسمّى صفائح التيار. من الممكن أن تقسم هذه الصفائح السائل إلى عدّة مجالات مغناطيسية، والتي تكون فيها التيّارات ضعيفة نسبيّاً. ويُعتقد أنّ صفائح التيار في الهالة الشمسيّة تتراوح بين بضعة أمتار وبضعة كيلومترات في السماكة، وهي رقيقة إلى حد ما مقارنة بالمجالات المغناطيسية (التي تتراوح بين آلاف ومئات الآلاف من الكيلومترات). وهناك مثال آخر في الغلاف المغناطيسي للأرض، حيث تفصل صفائح التيار مجالات مميزة من الناحية الطوبولوجية، مما يعزل معظم الغلاف الجوي للأرض عن الرياح الشمسية.

 

وتسمى صيغ الموجة المشتقّة باستخدام نظرية MHD البلازما بموجات المغناطيسية الهيدروديناميكية أو موجات MHD. بشكل عام هناك ثلاثة أنماط لموجة MHD:

 

موجة إلفين الخالصة (أو المائلة)

موجة MHD بطيئة

موجة MHD سريعة

 

كل الموجات السابقة لها سرعات طور ثابتة عند جميع الترددات وبالتالي لا يوجد أي تشتّت. وعند الحدود أي عندما تكون الزاوية بين متجه انتشار الموجة k والحقل المغنطيسي B إما (0) (180) أو (90) درجة، تُسمّى أوضاع الموجة.

 

سرعة المرحلة تتعلق بشكل مباشر بالزاوية بين شعاع الموجة المغناطيسية K والحقل المغناطيسي B، تنتشر موجة الـ MHD في زاوية عشوائية وتتعلق بالوقت وتراكم الحقل وحجمه B0 الذي يعوض تشتت الرابطة

ω k = v A cos ⁡ θ {\displaystyle {\frac {\omega }{k}}=v_{A}\cos \theta }

{\displaystyle {\frac {\omega }{k}}=v_{A}\cos \theta }

حيث

v A = B 0 μ 0 ρ {\displaystyle v_{A}={\frac {B_{0}}{\sqrt {\mu _{0}\rho }}}}

{\displaystyle v_{A}={\frac {B_{0}}{\sqrt {\mu _{0}\rho }}}}

هي سرعة إلفين، هذا الفرع يتوافق مع موجة إلفين القاصة. بالإضافة إلى ذلك تعطي معادلة التشتت العلاقة التالية{راجعها من اسفل الصفحة}:

ω k = [ 1 2 ( v A 2 + v s 2 ) ± 1 2 ( v A 2 + v s 2 ) 2 − 4 v s 2 v A 2 cos 2 ⁡ θ ] 1 2 {\displaystyle {\frac {\omega }{k}}=\left[{\frac {1}{2}}(v_{A}^{2}+v_{s}^{2})\pm {\frac {1}{2}}{\sqrt {(v_{A}^{2}+v_{s}^{2})^{2}-4v_{s}^{2}v_{A}^{2}\cos ^{2}\theta }}\right]^{\frac {1}{2}}}

{\displaystyle {\frac {\omega }{k}}=\left[{\frac {1}{2}}(v_{A}^{2}+v_{s}^{2})\pm {\frac {1}{2}}{\sqrt {(v_{A}^{2}+v_{s}^{2})^{2}-4v_{s}^{2}v_{A}^{2}\cos ^{2}\theta }}\right]^{\frac {1}{2}}}

حيث

v s = γ p ρ {\displaystyle v_{s}={\sqrt {\frac {\gamma p}{\rho }}}}

{\displaystyle v_{s}={\sqrt {\frac {\gamma p}{\rho }}}}

 

هي سرعة الصوت في الغاز المثالي. يتوافق فرع إشارة الموجب في المعادلة مع نمط موجة MHD السريعة بينما يتوافق الفرع ذو إشارة السالب في المعادلة مع وضع الموجة البطيئة MHD. سوف يتم تثبيط ذبذبات MHD إذا لم يكن السائل موصلا بشكل كامل إنّما موصليته محدودة، أو إذا كانت هناك تأثيرات لزجة.

 

تعتبر الموجات والتذبذبات MHD أداة شائعة للتشخيص عن بعد للبلازما المعملية والفيزياء الفلكية، على سبيل المثال. الهالة من الشمس (علم الزلازل الاكليلي). ستتثبّط ذبذبات الـ MHD إذا كان السائل ذو صلية محدودة وليس بشكل كامل، أو إذا تعرّض لعوامل لزجة.

 

تعتبر موجات وتذبذبات الـ MHD أداة شائعة للتشخيص عن بعد للبلازما المخبرية وبلازما الفيزياء الفلكية، على سبيل كمثال: هالة الشمس (علم الاهتزازات في الهالة الشمسية).

 

علاقة سرعة المرحلة مع الزاوية Θ في حالتين: الأولى VA > VS

اقرأ أيضا

 

شمس

نجم

اندماج نووي

مجرة

كلف الشمس

استشعار عن بعد

مسبار فضائي

مقراب جيمس ويب الفضائي

مرصد كيك

مقراب سبيتزر الفضائي

مرصد هابل الفضائي

الكيمياء الكهرومغناطيسية.

 

 

 ====نفس المقالة من ويكبيديا مفعلة الروابط والصور=============
نطاق صالح للحياة
من ويكيبيديا، الموسوعة الحرة
(بالتحويل من نطاق صالح للسكن)
اذهب إلى التنقل اذهب إلى البحث

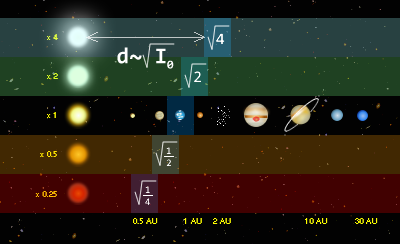
نماذج أنظمة تكون صالحة للحياة تعتمد على ضياء أنواع من النجوم
اَلْنِطَاقُ اَلصَّالِـحُ لِلْحَيَاةِ أو نِطَاقُ اَلْحَيَاةِ هو مصطلح في علم الفلك وعلم الأحياء الفلكي (بالإنجليزية: habitable zone) يشير إلى المنطقة حول نجم ما حيث يوجد كوكب له حجم كوكب الأرض وذو تركيب مشابه لها ويحتوي ماء على سطحه. وعلى اعتبار أن الماء هو عنصر أساسي لتواجد جميع أنواع الحياة، فتعتبر الكواكب الواقعة في هذا النطاق هي من الكواكب التي قد تتواجد عليها نوع من أنواع الحياة خارج كوكب الأرض. يعتمد ذلك النطاق من جهة أخرى على شدة أشعة النجم الواصلة إلى هذا النطاق حيث تكون في المتوسط نحو 10 درجات مئوية وكذلك على نوع الضوء الصادر منه، بحيث لا يغلب في طيفه مثلا أشعة فوق البنفسجية أو أشعة سينية، فكلاهما لا يصلح للحياة.
بالنسبة للشمس فيعتبر النطاق الصالح فيها للحياة بين الأرض أو أقصر قليلا بالنسبة للشمس والمريخ. فمثلا لا تصلح الزهرة للحياة حيث أنَّ درجة الحرارة عالية فيها، كما أنَّ فيها غازات ليست مناسبة للحياة. والكواكب الأبعد من المريخ فهي باردة جدا ولا يصلها من الطاقة الشمسية إلا القليل.
يمتد النقاش حول المنطقة الصالحة للحياة أيضا إلى مناطق في مجرة تكون قد تكوّن فيها عناصر ثقيلة مثل الكربون والأكسجين والنتروجين حيث تلك المكونات هي التي تبني أجسام الكائنات الحية وبالتالي تعيش عليها. يتكون من تلك العناصر وغيرها في البدء الكوكب الصالح للحياء في المنطقة الصالحة للحياة حول النجم، فيكون مماثلا لتركيبة الأرض. كما لا بد من الأخد في الحسبان ألَّا يتعرض هذا الكوكب الصالح للحياة نظريا إلى حدوث مستعر أعظم بالقرب منه فيميت بما يصدره من أشعة مميتة أي حياة قد تنشأ عليه.
نحن نتمتع على الكرة الأرضية بالحياة بعوامل مناسبة كثيرة. فالشمس نجم طويل العمر بمعنى أن الأرض في موقعها الحالي لديها زمن طويل مناسب لنشأة حياة عليها، فلو كان عمر الشمس مثلا 100 مليون سنة فهذا زمن قصير لا يكفي لنشأة حياة أو لو كانت حياة قد نشأت بالفعل فإنها تختفي مبكرا في مرحلة بدائية بسبب انتهاء عمر النجم نفسه.
ثانيا نشأت المجموعة الشمسية على أشلاء مستعر أعظم أو عدة مستعرات عظمى سبقت ومدت الأرض بتركيبتها هذه من جميع العناصر المعروفة لنا. فعمر المجموعة الشمسية نحو 5و4 مليار سنة، أي أنها من الجيل الثاني أو الثالث من النجوم من بعد نشأة الكون قبل نحو 7و13 مليار سنة. وبدأت الحياة على الأرض منذ نحو 3 مليارات سنة في حالة بدائية تطورت مع الزمن حتى حدث بما يسمى انفجار لللأحياء منذ نحو 500 مليون سنةٍ. الثدييات وأعلى مرتبة في تطور المملكة الحيوانية بدأ ظهورها منذ نحو 65 مليون سنة، كما أنَّ عمر الإنسان عليها لا يزيد عن نحو 5و1 مليون سنة.
ثالثا الشمس تعتبر مستقرة متوازنة الحرارة بمعنى أنها ليس لها نشاط تحمى فيه شديدا أو انفجارات فتميت الحياة على الأرض أو تضعف طاقتها كثيرا فتتجمد كل حياة على الأرض. كما أنَّنَا في منطقة بعيدة عن حدوث مستعرات حولنا تتسبب في القضاء على الأحياء. كما يحمي الغلاف الجوي للأرض الأحياء عليها من الأشعة فوق البنفسجية الضارة الآتية من الشمس. بالإضافة إلى ذلك فوجود القمر حول الأرض يجعل دورانها حول محورها مستقرا في الفضاء فتتمتع بتتابع فصول السنة بانتظام، فلو كان اتجاه محور دوران الأرض مهتزا أو متقلبا لما ساعد ذلك على نشأة الحياة التي نعرفها.
رابعا وليس أخيرا فتتمتع الأرض بمجال مغناطيسي يعمل على انحراف رياح شمسية عنا إلى أعماق الفضاء أو يهبط جزء من تلك الرياح الشمسية المكونة من جسيمات شديدة الطاقة مميته فوق قطبي الأرض بعيدا عن المناطق الآهلة بالحياة، في صورة ما يسمى الشفق القطبي.
محتويات 1 نطاق صالح للحياة 1.1 أهمية الماء
1.2 المناخ
1.3 أهمية المناخ
2 تقديرات للمجموعة الشمسية
3 المراجع
4 اقرأ أيضا
نطاق صالح للحياة
أهمية الماء
يعتمد النطاق الصالح للحياة حول نجم على درجة حرارة وضياء النجم الذي يدور الكوكب حوله، حيث تكون الطاقة الواصلة للكوكب كافية لأن يكون الماء في الحالة السائلة.
وفي نظرةٍ مبسطة يمكن افتراض أنه يمكن حساب هذا النطاق على أساس ضياء النجم. فينطبق على متوسط هذا النطاق حول نجم معين المعادلة التالية: d [ A E ] = L s t a r / L s u n {\displaystyle d[{\mathrm {A} E}]={\sqrt {L_{\mathrm {s} tar}/L_{\mathrm {s} un}}}} حيث: d {\displaystyle d} متوسط نصف القطر للنطاق الصالح للحياة وحدة فلكية، L s t a r {\displaystyle L_{\mathrm {s} tar}\,} الضياء البولومتري للنجم، L s u n {\displaystyle L_{\mathrm {s} un}\,} الضياء البولومتري للشمس (ضياء شمسي).المسافة AE تعادل وحدة فلكية = نحو 150 مليون كيلومتر (بعد الأرض عن الشمس).
فإذا كان ضياء النجم 25% من ضياء الشمس فسيكون النطاق الصالح للحياة لكوكب يدور حوله على بعد 5و0 وحدة فلكية، وإذا كان ضياء النجم ضعف ضياء شمسي فسيصبح النطاق الصالح للحياة على بعد 4و1 وحدة فلكية.
تلك هي نتيجة «قانون المسافة» المتعلق بضياء نجم. ومتوسط النطاق الصالح للحياة طبقا للتعريف هنا إنما هو بشرط أن يكون الكوكب له غلاف جوي مشابه لجو الأرض من وجهة التركيب والكثافة وفي حيز درجة حرارة عامة للكوكب مماثلة لدرجة حرارة جو الأرض بصفة عامة. حدود ذلك النطاق تكون محدودة بدرجة حرارة تجمد الماء ودرجة غليان الماء.
علاوةً على ذلك فتلعب تركيبة سطح الكوكب دورا هاما من حيث قدرتها على رد إشعاع النجم إلى الفضاء، كما تراعي الحسابات الحديثة تطور والتركيب الكيميائي للغلاف الجوي على الكوكب والانحباس الحراري فيه.
قام الفيزيائيان فيليب موريس و «جوزيبي كوكوني» ذلك النطاق لأول مرة في عام 1959 في تقرير بحث يسمى SETI (الذي يعتني بالبحث عن حياة خارج الأرض. وفي عام 1961 صاغ «فرانك دراكه» معادلة تسمى باسمه «معادلة دراكه».
ونظرا لتغير النجم وكذلك الكوكب مع الزمن فتتغير بذلك أيضا النطاق الصالح للحياة. فضياء النجم تقل مع الوقت بحسب تطوره. فلكي تنشأ حياة وتكون على الكوكب مشابهة للحياة على الأرض فقط فلا يكفي فقط بعده عن النجم، بل لا بد أيضا من أجتيازه فترة زمنية طويلة مماثلة لما حدث ويحدث على الأرض. أن يكون مدار الكوكب حول النجم دائما داخل الناق الصالح للحياة، وحتى لو قصرت المسافة بينهما مع الزمن فلا بد أن يستغرق ذلك طويلاً. وفي العادة يحتسب العلماء ما بين 4 و 6 مليارات سنة لتلك الفترة.
المناخ
تتطورت مناقشة العلماء بعد ذلك إلى مراعاة حسابات عن المناخ على الكوكب، وعلى الأخص الانحباس الحراري بسبب وجود ثاني أكسيد الكربون والماء.
فالانحباس الحراري على كوكب ليست عليه حياة ويكون في نطاق صالح للحياة تنظمه دورة كربونات و سيليكات: فنزول مطر محمل ب ثاني أكسيد الكربون في صورة حمض الكربونيك على السطح الصخري للكوكب حيث يذيب حمض الكربونيك السيليكات ويرتبط ثاني أكسيد الكربون في مركبات كالسيوم وسيليكات،
وتنتقل الصخور المحتوية على الكربون عن طريق العمليات التكتونية على سطح الكوكب وتنصهر إلى ماغما،
ثم يتسبب النشاط البركاني في تحرير ثاني أكسيد الكربون ثانيا إلى جو الكوكب.
تنظم تلك الدورة نفسها بنفسها حيث أنه عند انخفاض درجة الحرارة تنخفض أيضا كمية المطر، ويقل ثاني أكسيد الكربون في الجو عندما يقل النشاط البركاني. وعندما يزيد النشاط البركاني يزداد ثاني أكسيد الكربون في الجو، فيرتفع الانحباس الحراري وترتفع درجة حرارة الجو ثانيا. وعندما ترتفع درجة الحرارة فإنها تنظم الدورة من خلال زيادة في كمية المطر، فيقل ثاني أكسيد الكربون في الهواء وينخفض الانحباس الحراري. وتبلغ دورة الكربونات والسيليكات على الأرض عدة مئات آلاف من السنين.
يعرّف الحد الأدنى للنطاق الصالح للحياة على أساس شدة الانحباس الحراري فقد ترتفع درجة الحرارة على الكوكب بحيث يتطاير الماء وينتشر في الفضاء البين كوكبي، وتنتهي بذلك دورة الكربونات والسيليكات نهائيًا. بالنسبة لذلك الحد الأدنى للنطاق الصالح للحياة على الأرض فهو يبلغ نحو 95و0 وحدة فلكية. وعندما يكون الكوكب عند الحد الخارجي للنطاق الصالح للحياة فلا يمكن لسحب من ثاني أكسيد الكربون المتكثف أن تزيد من درجة حرارة الكوكب عن طريق الانحباس الحراري بالدرجة الكافية. بالنسبة لذلك الحد في المجموعة الشمسية فهو يقع عند نحو 4و1 وحدة فلكية.
في المجموعة الشمسية توجد الأرض وحدها فقط داخل هذا النطاق حول الشمس. الزهراء وعطارد يعتبران قريبين من الشمس وتكون الحرارة عالبية عند هذا الحد. ويقع المريخ داخل تلك المنطقة أو خارجها قليلا وذلك بحسب نموذج الحساب المأخوذ في الاعتبار. وقد يكون قد مر على المريخ زمن كان الانحباس الحراري عليه مناسبا. ولكن المريخ كوكب صغير لا يسمح لنشاط تكتوني لمدة مليارات من السنين. بذلك يعتبر المريخ قد فقد عنصرا من عناصر التوازن المناخي بعد تصلب السطح الصخري عليه، وافتقد نشاطه البركاني، وبالتالي افتقد دورة الكربونات والسيليكات، فلم يحدث عليه توازن في المناخ لمدة طويلة.
يمكن لكوكب بحجم كتلة الأرض أن يكون صالحا للحياة إذا كان على بعد المريخ، هذا يختلف بحسب النموذج الحسابي المأخوذ في الاعتبار. أما إذا كان الكوكب على بعد مثل بعد المشتري عن الشمس فإن ما يصله من طاقة من الشمس لا يكون كافيا ليصهر الثلج بحيث يكون ماء سائلا صالحا للحياة.
أهمية المناخ
تقديرات للمجموعة الشمسية

النطاق الداخلي الصالح للحياة (أخضر غامق) والنطاق الخارجي (أخضر فاتح) لنظام المجموعة الشمسية .
تصل تقديرات النطاق الصالح للحياة في المجموعة الشمسية بين 725و0 إلى 0و3 وحدة فلكية اعتمادا على نماذج علمية مختارة:
حيث: AU: وحدة فلكية = نحو 150 مليون كيلومتر (= بعد الأرض عن الشمس).
الحد الداخلي الحد الخارجي المرجع ملاحظات
0,725 AU 1,24 AU Dole 1964
اعتبار غلاف جوي خفيف ونفاذ للضوء.
0,95 AU 1,01 AU Hart et al. 1978, 1979
نجوم من تصنيف K0
0,95 AU 3,0 AU Fogg 1992
مراعاة دورات ثاني أكسيد الكربون.
0,95 AU 1,37 AU Kasting et al. 1993
– 1%...2% أبعد إلى الخارج Budyko 1969
... يعم الثلج سطح الأرض.
– 1%...2% أبعد إلى الخارج Sellers 1969
... يعم الثلج سطح الأرض.
– 1%...2% أبعد إلى الخارج North 1975
... يعم الثلج سطح الأرض.
4%...7% أقرب – Rasool & DeBurgh 1970
... عدم تكثف ماء المحيطات.
أمثلة على نطاقات صالحة للحياة بالقرب من نجوم أخرى من نجوم النسق الأساسي:
تصنيف الطيف AU وحدة فلكية
O6V 450 - 900
B5V 20 - 40
A5V 2,6 - 5,2
F5V 1,3 - 2,5
G5V 0,7 - 1,4
K5V 0,3 - 0,5
M5V 0,07 - 0,15
============
كلفة شمسية
من ويكيبيديا، الموسوعة الحرة
(بالتحويل من كلف الشمس)
اذهب إلى التنقل اذهب إلى البحث
فيزياء شمسية

R C F = R P ( B s u r f 2 μ 0 ρ V S W 2 ) 1 6 {\displaystyle R_{CF}=R_{P}\left({\frac {B_{surf}^{2}}{\mu _{0}\rho V_{SW}^{2}}}\right)^{\frac {1}{6}}}
كلفة شمسية
وهج الشمس
الفروع
مجالات البحث
التجارب الحالية
العلماء
هذا الصندوق: اعرض
ناقش
عدل
الكلفة الشمسية أو البقعة الشمسية (بالإنجليزية: Sunspot)‏ هي بقع على سطح الشمس -الغلاف الضوئي Photosphere - تتميز بدرجة حرارة منخفضة عن المناطق المحيطة بها وبنشاط مغناطيسي مكثف يمنع حمل الحرارة، مكونا مناطق ذات حرارة سطحية منخفضة.
وبالرغم من كونها مناطق شديدة السطوع إلا أن الفرق بين درجة حرارتها، التي تبلغ حوالي 4000-4500 كلفن وحرارة سطح الشمس عموما (5700 كلفن)، تجعلها تظهر كبقع مظلمة. ولو نظرنا إلى هذه البقع بمعزل عن الغلاف الضوئي المحيط بها لبدت أكثر سطوعا من المصباح القوسي. ولقد بلغت البقع الشمسية حدا أدنى خلال دورة الكلف الشمسية في عام 2009م.[1]
محتويات 1 التكوين
2 سطح الشمس
3 البقع الشمسية
4 اكتشاف الكلف الشمسي
5 القوة المغناطيسية
6 معرض صور
7 اقرأ أيضا
8 مصادر
9 وصلات خارجية
التكوين
تتكون البقع الشمسية على فترات تمتد من أيام إلى أسابيع، ويمكن أن تتمتد لأشهر، متوسط عدد البقع الشمسية التي يمكن رؤيتها على سطح الشمس ليس دائما نفسها، لكن يذهب صعودا وهبوطا في الدورة الشمسية الواحدة.
يعتبر الحد الأقصى للطاقة الشمسية أو الطاقة الشمسية القصوى هي فترة النشاط الشمسي الأكبر في الدورة الشمسية للشمس، إذ تبلغ مدة الدورة الشمسية الواحدة حوالي 11 عاماً. تتكون البقع الشمسية من جزأيين: الجزء المظلم (اومبرا)
الجزء حول الجزء المظلم ( بينومبرا)
سطح الشمس
الشمس عبارة عن نجم مكون من غاز ساخن جدا، والطبقة الخارجية للشمس هي التي تسمى المتكور المضئ (الفوتوسفير) وهي سطح الشمس المضيء، وتصل درجة حرارته 5800 درجة كلفن، ويبدو حبيبيا خشنا كأنه مكون من ملايين الحبات من حبة الأرز، ناشئة عن الحمل الحراري الذي يحدث في طبقة تحت السطح تنتقل فيها الحرارة من باطن الشمس إلى السطح. وتظهر البقع دوريا على سطح الشمس كل نحو 11 سنة، وتكثر البقع الشمسية في المناطق الوسطية من الشمس. ومناطق البقع الشمسية تتميز بدرجة حرارة أقل من المناطق الشاملة للسطح (تبلغ 4500 كلفن تحيطها مناطق تبلغ حرارتها 5800 كلفن). والبقع عبارة عن ثقوب في سطح الشمس يتدفق منها الغاز والحرارة والإشعاع من داخلها تحت تأثير المجال المغناطيسي، وتسمى هذه البقع كلف الشمس.
تدور الشمس حول محورها تماما مثل ما تفعل الأرض، ويوجد مظاهر شمسية على الشمس مثل مناطق البقع الشمسية التي تتبع حركة دوران الشمس، وهذا يعني أن البقع الشمسية تنتقل عبر القرص الشمسي من الشرق إلى الغرب كما تتم رؤيتها من الأرض.
وتأخذ البقع الشمسية حوالي أسبوعين للانتقال من الطرف الشرقي إلى الطرف الغربي على سطح الشمس. الشمس ليس النجم الوحيد الذي يحدث على سطحه بقع شمسية، وقد تمكن علماء الفلك من اكتشاف بعض البقع النجمية على النجوم الأخرى.
البقع الشمسية
ويكون عدد هذه البقع الشمسية أكثر منه في أحيان أخرى، وفي مدى كل عشر سنوات أو إحدى عشر سنة، كما في السنوات 1937م، 1947م، 1958م. وقد تمكن العلماء مشاهدة وجود بقع من كلف الشمس بأعداد كبيرة جدا.
ولهذه الكلف السوداء التي تقع على سطح الشمس أشكال متنوعة، وإذا واصلنا مراقبتها يوما بعد الآخر وجدنا إنها تتحرك على سطح الشمس، ولكن هذا يدل في حقيقته على دوران الشمس حول نفسها، وبمراقبة الكلف الشمسية تمكن العلماء من حساب سرعة دوران الشمس حول محورها، والوقت الذي تستغرقه لذلك.
من الممكن أن تحتوي الشمس على مئات البقع الشمسية في فترات، ومن الممكن أن لا تحتوي على أيٍ منها خلال فترات أخرى. وذلك عائدُ إلى أن البقع الشمسية لها دورات تظهر من خلالها وهذه الدورات تحدث خلال 11 سنة. فعلى سبيل المثال للدورة: خلال السنة الأولى لا تحتوي الشمس على أي بقع وبعد خمس سنوات ونصف سوف تحتوي الشمس على أعلى عدد من البقع وتقل تلك البقع حتى اختفاء البقع بعد خمس سنوات ونصف أخرى.
اكتشاف الكلف الشمسي
قديما حوالي سنة 28 قبل الميلاد عمل أحد علماء الفلك الصينيين الذي كان يسجل أي حركة غير عادية وملحوظة تظهر في السماء على تسجيل وجود بقع داكنة من وقت لأخر على وجه الشمس، ولقد أكدت المراقبة بالمقراب لاحقا في سنة 1611م، أن هذه البقع موجودة حقا رغم أن طبيعتها ظلت غامضة.
ومنذ تلك الأيام علمت المراقبة المنتظمة علماء الفضاء الكثير عن البقع الشمسية التي هي برهان مرئي على النشاط المتواصل للغلاف الشمسي فوتوسفير أو السطح المرئي للشمس. ويتراوح قطر هذه البقع بين 960 كلم إذا كانت منفردة و96 ألف كلم إذا كانت مجموعة بقع. وأكبر مجموعة بقع شمسية تم تسجيل وجودها حتى اليوم في شهر ابريلمن عام 1947، حيث كان قطرها حوالي 130 ألف كلم.
والبقعة الشمسية هي في الواقع مساحة من الغاز تكون أبرد من المساحة المحيطة بها من السطح المرئي للشمس ويظن أنها ناتجة عن حقول مغناطيسية قوية تسد التدفق الخارجي للحرارة إلى الغلاف الضوئي (سطح الشمس) من داخلها. وتتكون هذه البقع من مواضع مظلمة نسبيا، تبلغ درجة حرارتها نحو 4000 درجة كلفن (K) أي ما يقارب 3700 درجة مئوية، بعضها يكون شبه مظلم تبلغ حرارته 5500 درجة كلفن، هذا بالمقارنة بدرجة حرارة سطح الشمس البالغة 5700 كلفن.
القوة المغناطيسية
المجالات المغناطيسية الواقعة على السطح المرئي (الفوتوسفير) للشمس والتي تولد البقع الشمسية قوية للغاية تبلغ عشرة آلاف مرة أقوى من المجال المغناطيسي لسطح الأرض، ويتطور مركز نشاط البقعة الشمسية على عدة مراحل بدءا من تكوين مجال مغناطيسي ثنائي القطب مرفق عادة بظهور مفاجئ لبقعة براقة صغيرة تسمى الشعلة Faculae أو بتعبير علمي صيخدا الشمس، وكلمة Faculae المستمدة من كلمة لاتينية تعني المشاعل هي صياخد الشمس وتم اكتشافها باكراً في القرن السابع عشر من جانب عالم فلك ألماني اسمه كريستوف شاينر وتعرف هذه البقع الآن بأنها عبارة عن سحابات غازية مضيئة مكونة أساساً من الهيدروجين وتقع فوق السطح المرئي للشمس قليلا. وتكمن العلاقة بين المجال المغناطيسي وظهور البقع الشمسية في أن القوة المغناطيسية والتي تظهر على هيئة خطوط مغناطيسية تمنع تدفق البلازما شديدة الحرارة من دخول منطقة الواقع عليها المجال وبالتالي تنخفض درجة حرارة تلك المنطقة عن ماحولها، فتظهر على هيئة بقع شمسية.
معرض صور






========
دورة شمسية
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث

دورات النشاط الشمسي منذ عام 1975.تستغرق الدورة نحو 11 سنة.
الدورة الشمسية ([الإنجليزية: Solar cycle) هو التغير الدوري في النشاط الشمسي بما في ذلك التغيرات في مستويات الإشعاع الشمسي ، وكذلك تغيرات في مظهر الشمس ، مثل البقع الشمسية ووهج الشمس . تمتد الدورة الشمسية لمدة حوالي 11 عاما ، وهي تختلف ما بين 9 سنوات إلى 13 سنة . وقد رصدت هذه الدورات منذ مئات السنين اعتماداً على تغير عدد البقع الشمسية ، وظهور الشفق القطبي على الأرض . حديثا ومنذ استخدام الأقمار الصناعية وكثرة استخدام الترانزيستور نلاحظ تأثيرات النشاط الشمسي في الإضرار بأجهزة الأقمار الصناعية والأجهزة الكهربائية ، وأحيانا تتسبب في انقطاع التيار الكهربائي ، مثلما حدث في كندا وشمال شرق الولايات المتحدة في 1 و 2 سبتمبر عام 2003.
تؤثر الدورة الشمسية طفيفا على المناخ على الأرض ، ويعتقد بعض العلماء أن لها تأثير على نمو الأشجار .
لمحة تاريخية
تم اكتشاف الدورة الشمسية في عام 1843 من قبل صموئيل هاينريش شواب. فبعد 17 عاماً من المشاهدات لاحظ وجود اختلاف في متوسط عدد البقع الشمسية على قرص الشمس من سنة إلى أخرى . أحصى رودولف وولف هذه التغيرات وغيرها من الملاحظات ، وأعاد دراسة الدورة الشمسية رجوعاً حتى دورة عام 1745.
حتى وقت قريب كان يُعتقد أن عدد الدورات الشمسية في ال309 سنة الأخيرة (مابين 1699-2008) يصل إلى 28 دورة شمسية، مما جعل متوسط الدورة 11.04 سنة. لكن أظهرت الأبحات الحديثة أن الدورة الطويلة المفترضة مابين عامي (1784-1799) كانت عبارة عن دورتين.
مما جعل متوسط الدورة 10.66 سنة. وبلغت أطول دورة شمسية 14 عام و أقصرها 9 سنوات. كما يشير مصطلح ذروة الدورة الشمسية وقاع الدورة الشمسية إلى العدد الأكبر والعدد الأقل للبقع الشمسية المرصودة على القرص الشمسي.
وضح الأساس الفيزيائي للدورة الشمسية في أوائل القرن العشرين بواسطة جورج هيل وفريقه، حيث أظهر أن البقع الشمسية ممغنظة بشكل شديد (كان هذا أول اكتشاف لحقل مغناطيسي خارج الأرض) ، وبيّن في عام 1919 أن الحقول المغناطيسية على الشمس ثنائية الأقطاب ولديها الخصائص التالية: يكون الواد منهم دائماً في نفس نصف الكرة الشمسي أثناء ظهور البقع الشمسية
ينعكس هذا الحقل من دورة بقع شمسية إلى أخرى.
انظر أيضاًنشاط شمسي
فيض راديوي شمسي
=====
نشاط شمسي
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
فيزياء شمسية

R C F = R P ( B s u r f 2 μ 0 ρ V S W 2 ) 1 6 {\displaystyle R_{CF}=R_{P}\left({\frac {B_{surf}^{2}}{\mu _{0}\rho V_{SW}^{2}}}\right)^{\frac {1}{6}}}
كلفة شمسية
وهج الشمس
الفروع
مجالات البحث
التجارب الحالية
العلماء
هذا الصندوق: اعرض
ناقش
عدل

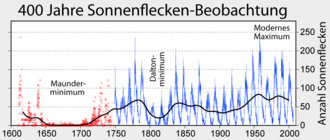
تغير أعداد البقع الشمسية في كل دورة منذ عام 1610 .

شدة اشعاع الشمس خلال النشاطات الشمسية منذ عام 1975 (أنظر أيضا فيض راديوي شمسي).

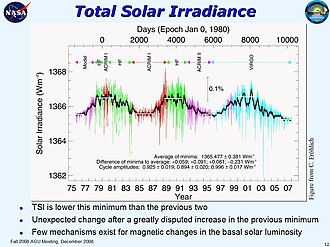
نصيب الأرض من الأشعة الشمسية عبر 3 دورات للنشاط الشمسي (منذ عام 1975) . المحور العمودي بوحدة واط/متر مربع.
نشاط شمسي يقصد بالنشاط الشمسي تغيرات دورية في خواص الشمس ويكون مقترنا بأعاصير من غازاتها الساخنة وتغيرات مستمرة في مجالها المغناطيسي. ويظهر هذا النشاط الشمسي في زيادة واضحة للبقع الشمسية ومواقعها عبر الدائرة الاستوائية للشمس. وتبلغ دورة البقع الشمسية في المتوسط نحو 11 عاما ن وقد تتغير الدورة فيما بين 9 إلى 13 عام. ويصل متوسط عدد البقع الشمسية بين 0-5 في حالة عدم النشاط إلى نحو 100 بقعة أو أكثر في وقت النشاط (وصل عدد البقع الشمسية نحو 200 بقعة في نشاطها عام 1960 .
بالإضافة إلى تلك الظاهرة تحدث أنبعاثات غازية وإشعاعية غير منتظمة في هيئة انفجارات شمسية، وتغيرات في ريح شمسية وبعض الأعاصير الشمسية ووابلات من البروتونات، كما تحدث من غير انتظام نافورات غازية هائلة.
ومع أن درجة حرارة البقع الشمسية تكون أقل بنحو 1000 درجة من بقية سطح الشمس إلا أن الشمس تشع طاقة أكبر نسبيا أثناء فترة نشاطها بالمقارنة بفترة ركودها. تنتج تلك الطاقة الزائدة من المناطق الأكثر سخونة من تلك البقع الشمسية. وتؤثر البقع الشمسية على الجو والطقس على الأرض، كما تؤثر على الأقمار الصناعية، وكذلك على الأجهزة الإلكترونية على الأرض. وتؤثر البقع الشمسية على الشفق القطبي، وعلى الطبقة الجوية المتأينة (أيونوسفير)، وبالتالي تؤثر على الاتصالات اللاسلكية وإرسال الراديو والتلفزيون.
محتويات 1 قياس النشاط الشمسي 1.1 عدد البقع الشمسية
1.2 شدة الإشعاع الراديوي
2 الدورات
3 طيف النشاط الإشعاعي
4 غازات ساخنة، انفجارات، وشفق قطبي
5 اقرأ أيضا
6 مراجع
قياس النشاط الشمسي
عدد البقع الشمسية
منذ اكتشاف البقع الشمسية في عام 1610 بدأ الأهتمام بمشاهدتها على الدوام، وتعد تلك الظاهرة من أطول الفترات التي طبقت فيها طرق قياس علمية مستحدثة. ومن أسهل القياسات الممكن عملها هو تحديد عدد البقع الشمسية وتسجيلها: R = k ( 10 g + f ) {\displaystyle \mathrm {R} =\mathrm {k} (10\,\mathrm {g} \,+\,f)}
حيث: k معامل يعتمد على التلسكوب المستخدم،g عدد «مجموعات البقع»و f عدد البقع المنفردة.
ومنذ عام 1970 بدأت مجموعة من المراصد ترصد الشمس يوميا وتعيين المساحة الكلية للبقع الشمسية. وتبين تلك الطرق المسهبة للقياس تقريبا نفس ما يأتي به الطريقة البسيطة «طريقة تعيين عدد البقع».
شدة الإشعاع الراديوي
المقالة الرئيسة: فيض راديوي شمسي
طريقة إضافية لقياس النشاط الشمسي هي قياس شدة الأشعة الراديوية القادمة من الشمس عند طول موجة قدرها 7و10 سنتيمتر. وتتناسب شدة هذه الأشعة مع عدد البقع الشمسية، وتعين بواسطة مراصد علم الفلك الراديوي.
الدورات
تستغرق أوضح دورات النشاط الشمسي نحو 11 سنة وتسمى أيضا «دورة شواب» نسبة إلى مكتشفها «صمويل هانريش شواب»، العالم الفلكي الألماني. تتبع قمم النشاط الشمسي تك الدورات الزمنية وهي متغيرة في حدود بين 9 إلى 13 سنة.
استطعنا عن طريق قياس تأثير زيمان معرفة أن البقع الشمسية نتيجة لتغير المجال المغناطيسي للشمس كما نستطيع قياس قطبية المجال المغناطيسي عليه. واتضح أن القطبية المغناطيسية للبقع الشمسية تزداد من دورة لدورة في أحد نصفي الكرة الشمسية. وعلي دلك فيبدو أن هناك دورة أكبر أكبر قدرها 22 سنة، وتسمى «دورة هيل» Hale-Zyklus.
ويبدو أن هناك دورات أخرى مثل «دورة جلايسبرج» وهي تستغرق بين 80 - 90 سنة، وقد اكتشفها الفلكي الألماني أيضا «ولفجانج جلايسبرج».
وبسبب المشاكل الذي يسببه النشاط الشمسي لبعثات الفضاء عندما يزداد نشاطها فإن التوقع بحدوثها يزداد أهمية. وقد طور ولفجانج جلايسبرج طريقة لتوقعها عن طريق مقارنته عدة دورات متعاقبة للنشاط الشمسي.
طيف النشاط الإشعاعي

الطيف الشمسي (العادي) فوق الغلاف الجوي للأرض ،و عند سطح البحر (أحمر)، (الفجوات على الأرض بسبب امتصاص الهواء لبعض الأشعة بحسب طول موجتها ) .
منذ عدة عشرات السنين اكتشفت فيزياء الشمس أن النشاط الشمسي يصدر طيفا للأشعة الكهرومغناطيسية مغايرا لطيف الضوء المعتاد، ومن ضمنها فيض الشمس الراديوي والذي يستخدم كمؤشر للنشاط الشمسي، ويتعلق به الشفق القطبي.
تنشأ الطاقة الضوئية للشمس من الاندماج النووي للهيدروجين حيث يندمج في قلب الشمس إلى هيليوم وتنتقل الحرارة عن طريق نيوترينوات، وانتقال الحرارة بالإشعاع، وبالحمل إلى السطح.
من تداخل تلك المؤثرات مع بعضها البعض ينتج طيفا اشعاعيا يمتد من نطاق الأشعة فوق البنفسجية إلى نطاق الضوء المرئي إلى الأشعة تحت الحمراء إلى نطاق الأشعة الراديوية. وتوجدعلى الشمس حينئذ مناطق كبيرة وصغيرة ذات درجات الحرارة مختلفة، وانبعاثات غازات، وأعاصير أشعاعية متفرقة بعضها يصدر أشعة إكس، والآخر يصدر أشعة فوق بنفسجية أو أشعة راديوية.
غازات ساخنة، انفجارات، وشفق قطبي

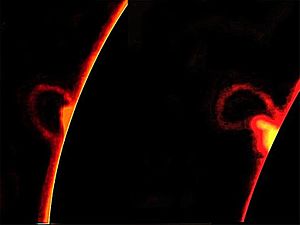
انفجارات شمسية.

حلقات مغناطيسية على سطح الشمس.
تنشأ مجالات مغناطيسية هائلة مع البقع الشمسية الكبيرة من النوعين (Type E, Type F)، وفي أمكانها أطلاق سحب غازات ساخنة من طبقات الشمس العليا إلى الفضاء. وتكون تلك الغازات الساخنة مشحونة كهربائيا وتحدث إضطرابا عند ملاقاتها المجال المغناطيسي لكوكب الأرض، حيث تصلنا من الشمس خلال عدة أيام قليلة.
أما الانفجارات الشمسية فهي انفجارات فجائية تحدث في طبقات الشمس العليا وتستمر بين عدة دقائق إلى عدة ساعات. تنطلق خلالها أشعة غاما الشديدة، وأشعة فوق البنفسجية، واشعة راديوية. كما يصحبها جسيمات أولية ذات طاقة عالية (إلكترونات وبروتونات، وأنوية الهيليوم).

شفق قطبي كما رؤي في النرويج.
لا نشعر بزوابع مغناطيسية على الأرض بسبب الشمس، ولكن إذا حدثت أعاصير مغناطيسية شديدة على الشمس فهي تؤثر على الأقمار الصناعية وقد تفسد بعض أجهزتها، كما يمكنها أن تشوشر على الأجهزة الكهربائية وعلى الاتصالات اللاسلكية، وقد حدث ذلك في السنوات الماضية. وبينما تكون الأعاصير المغناطيسية الشديدة على الشمس لا تشكل تهديدا للحياة على الأرض، إلا أنها تؤثر على رواد الفضاء أثناء رحلاتهم الفضائية الطويلة.
وطبقا لتقريرات مركز البحوث الجغرافي في بوتسدام (ألمانيا) كان أشد إعصار مغناطيسي على الشمس خلال يومي 1 و 2 سبتمبر 1859 تسببت في تعطيل خط التلغراف المعمول جديدا في ذلك الوقت، كما أنتج شفقا قطبيا ظهر حتى في روما وهافانا. كذلك في خريف عام 2003 شوهد الشفق القطبي في جنوب ألمانيا وفي النمسا.
وتقوم مراصد الشمس برصد البقع الشمسية والانفجارات التي تحدث على سطح الشمس وكذلك مراقبة تشكيلا الهالة الشمسية. كما ترسل الأقمار الصناعية الخاصة تقوم برصد سحب الغازات الكبيرة على الشمس وتتبع الانفجارات وترسل بياناتها إلى الأرض قبل وصول تلك التأثيرات بمدة طويلة. كذلك يأمل العلماء أن يحصلوا من القمرين الصناعيين ستريو -المرسلين بالقرب من الشمس - أن يحصلوا على معلومات عم فيزياء الشمس وعن حالاتها الغير عادية.
يعتقد بعض العلماء ومن ضمنهم «أندرو دوجلاس» أن نمو الأشجار يتأثر بنشاط الشمس، ولا يزال البحث جاريا للتحقق من ذلك.
=========
هالة (فضاء)
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
لمعانٍ أخرى، طالع هالة (توضيح).
ميّز عن هالة ضوئية.

هالة الشمس خلال كسوف الشمس عام 2006.

الهالة الشمسية كما ظهرت خلال كسوف الشمس عام 1999.
هالة الشمس (بالإنجليزية: Corona)‏ هي منطقة «جو» خفيفة ناصعة محيطة بالشمس، لا يمكن رؤيتها إلا في وقت الكسوف الكلي للشمس. وتمتد الهالة إلى نحو 1 - 3 من قطر الشمس خارجها وتمثل منطقة وسطية بين الشمس والفضاء الخارجي. ويستطيع العلماء قياس المنطقة الداخلية للهالة في جميع الأوقات بدون الانتظار حتى حدوث الكسوف، وذلك بوضع قطعة معدنية مستديرة صغيرة في التلسكوب تحجب الشمس نفسها كما يحدث في الكسوف.وترجع الصفات الطيفية غير العادية للهالة الشمسية إلى درجة حرارة العالية، مما دعا بعض علماء القرن التاسع عشر إلى الاعتقاد بتواجد عنصر غير معروف فيها أسموه كورونيوم. ثم بينت القياسات والبحوث العلمية بعد ذلك أن هذا الطيف الغريب يعود إلى الحديد شديد التأين (Fe-XIV)، والذي يتسبب في ارتفاع درجة الحرارة خارج الشمس في الهالة إلى 1 - 2 مليون درجة مئوية.
محتويات 1 هالة ساخنة
2 تفسيرها
3 اللمعان الكلي للهالة
4 التكوين الطيفي للهالة
5 اقرأ أيضا
6 مراجع
7 مصادر
8 روابط خارجية
هالة ساخنة

أثناء انفجار شمسي حدث في مارس 2012 نتج عنه انبعاث كتلي إكليلي، هذا الانفجار الشمسي ليس متجها إلى الأرض وبالتالي فهو لا يؤثر عليها.

حلقات مغناطيسية في الهالة.
يقع الغلافان الشمسيان الغلاف اللوني والغلاف الضوئي أسفل من الهالة. وتتكون الهالة من غازات متأينة في حالة بلازما وتتميز الهالة بأن درجة حرارتها أعلى كثيرا من الغلافين الأسفل منها وتصل درجة حرارتها عدة ملايين كلفن. في حين يبلغ درجة حرارة سطح الشمس نحو 5780 درجة فقط. أسباب نشأة الهالة وآليات تكوّن درجة الحرارة العالية فيها لا تزال غير مفهومة تماما ويبحث فيها العلماء سواء بالمراصد الأرضية أو بمراصد ترسل على أقمار صناعية.ويتبوأ فرع الفيزياء الخاص «بفيزياء الشمس» أهمية خاصة لدى العلماء حيث يؤثر النشاط الشمسي وظهور البقع الشمسية تأثيرا مباشرا على الأحوال على الأرض وأحيانا تحدث عواصف شمسية تؤدي إلى أصابة الأرض بوابل من الجسيمات تتسبب في انقطاع التيار الكهربائي في بعض أنحاء العالم مثلما حدث في كندا في سبتمبر 2003، كما تهدد تلك الجسيمات السريعة صحة رواد الفضاء وأحيانا تفسد أجهزة الأقمار الصناعية. لهذا تهتم فيزياء الشمس بإرسال مراصد قريبة منها لدراستها، دراسة الهالة الشمسية ودراسة النشاط الشمسي.في أوقات النشاط الشمسي قد تمتد الهالة المرئية إلى عدة ملايين كيلومترات وبالتالي قد تبلغ 2 إلى 3 قطر شمسي فوق الغلاف الضوئي (سطح الشمس). وتظهر الهالة في هيئة إشعاعية إلى الخارج بسبب مغناطيسية الهالة وتتغير كل 11 سنة مع دورة النشاط الشمسي. وبسبب التشكيلات المختلفة للمجال المغناطيسي والتي توجد فيها البلازما، فإن الأشعة المرئية تظهر أثناء قمة النشاط الشمسي في جميع الاتجاهات حول الشمس بينما أثناء فترات الهدوء فيغلب وجود الهالة عبر الدائرة الاستوائية للشمس.
تفسيرهاتوجد عدة نماذج فيزيائية تفسّر تسخين الهالة الشمسية، حيث تصل درجة الحرارة فيها عدة ملايين درجة بينما لا تتعدى درجة حرارة سطح الشمس 5800 درجة. ومن تلك النماذج تشتت موجات البلازما (جسيمات أولية مشحونة) وتغيرات مستمرة في أشكال الحقول المغناطيسية على الشمس، وانتشار تصادمي لتيارات كهربائية، وتسخين من خلال موجات تصادمية وبعض التأثيرات الأخرى. وقد ساهمت في الحصول على تلك النتائج عدة أقمار صناعية قامت بالرصد، مثل «مرصد الشمس وغلافها» سوهو ومسبار تريس ومرصد شاندرا الفضائي للأشعة السينية والقمر الصناعي RHESSI. كما سوف يقوم «مسبار الشمس +» مسبار باركر أثناء وجوده في فلك حول الشمس على بعد نحو 4 أقطار من الشمس بقياسات في الهالة.

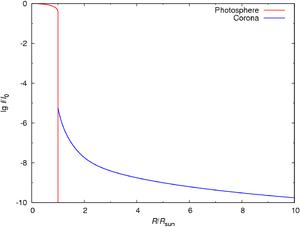
المنحنى الضوئي اللوغاريتمي لهالة الشمس (أزرق). ويمثل المنحنى الأحمر الغلاف الضوئي للشمس وانخفاض اللمعان بالابتعاد عن سطح الشمس.
يوجد تدرج شديد في درجة الحرارة في المنطقة التحتية من الهالة حيث تنخفض فيها الكثافة بالابتعاد عن سطح الشمس (أنظر الشكل). وخلال عدة مئات الكيلومترات فوق السطح ترتفع طاقة الحركة لجسيمات البلازما إلى نحو مليون درجة مئوية. وتتسبب درجة الحرارة العالية وبعض آليات التسارع إلى نشأة الريح الشمسية التي تنتشر في الفضاء. وينشأ تسارع الجسيمات المشحونة عن تواجدها في موجات أو أعاصير مغناطيسية شديدة تعمل على تسريع جسيمات البلازما المتكونة بصفة أساسية من بروتونات وإلكترونات.
كما يرجع سبب تسخين الهالة إلى تلك الدرجات العالية كون كثافتها منخفضة جدا. وتمثل درجة حرارتها العالية ما يكتسبه أي غاز أو البلازما من طاقة حركة لجسيماته. فإذا وجد جسم صلب على نفس البعد من الشمس فستكون درجة حرارته أقل بكثير، حيث يحدث فيه توازن حراري مختلف تماما عن التوازن الحراري في غاز أو بلازما.
وتصف المعادلة التقريبية التالية شدة إشعاع الهالة كما يرجع سبب تسخين الهالة إلى تلك الدرجات العالية كون كثاقتها منخفضة جداً. وتمثل درجة حرارتها العالية ما يكتسبه أي غاز أو البلازما من طاقة حركة لجسيماته. فإذا وجد جسم صلب على نفس البعد من الشمس فستكون درجة حرارته أقل بكثير، حيث يحدث فيه توازن حراري مختلف تماما عن التوازن الحراري في غاز أو بلازما.
وتصف المعادلة التقريبية التالية شدة إشعاع الهالة (Lit.: November & Koutchmy, 1996) خارج الشمس بالنسبة لدرجة إشعاع قرص الشمس نفسه ابتداء من مركز فرص الشمس: I ( ρ ) I ( 0 ) = 10 − 6 ( 3,670 ρ 18 + 1,939 ρ 7 , 8 + 0,055 1 ρ 2 , 5 ) ρ > 1 {\displaystyle {I(\rho ) \over I(0)}=10^{-6}\left({\frac {3{,}670}{\rho ^{18}}}+{\frac {1{,}939}{\rho ^{7{,}8}}}+{\frac {0{,}0551}{\rho ^{2{,}5}}}\right)\;\quad \rho >1}
حيث ρ {\displaystyle \rho } هي مسافة بدون وحدات من مركز الشمس، وهي تساوي هنا ρ = 1 {\displaystyle \rho =1} عند حافة الشمس.
تمثل تلك المعادلة التقريبية متوسط زمني ومكاني لأن شدة إشعاع الهالة يعتمد اعتمادا قويا على خطوط العرض على الشمس وعلى النشاط الشمسي وقت المشاهدة.
اللمعان الكلي للهالةبإجراء التكامل للمعادلة السابقة من حافة الشمس ρ = 1 {\displaystyle \rho =1} حتى مالانهاية نحصل على اللمعان الكلي للهالة، وذلك عند حدوث خسوفا كليا للشمس. ويبلغ اللمعان الكلي للهالة نحو 1,6 · 10−6 من الضياء الكلي للشمس، أو من قدرها الظاهري البالغ −12m,3. ذلك المعان ضعيف وهو يعادل القدر الظاهري للمعان القمر عندما يكون بدرا. ولذلك فإننا نستطيع مشاهدة الهالة أثناء الخسوف الكلي للشمس من دون لوح غامق واقي للعين. وبمجرد أن يتزحزح القمر عن الشمس ويظهر خلفه هلال رفيع من الشمس تختفي الهالة عن أعيننا بسرعة. وعندئذ لا بد من استخدام واقي للعينين لمتابعة مشاهدة الخسوف.
التكوين الطيفي للهالة
يتكون ضوء هالة الشمس من ثلاثة أجزاء أساسية، تظهر في التحليل الطيفي: الهالة F : ويتكون ضوؤها من ضوء الشمس المنعكس على غبار، وتسمى خطوطها الطيفية بأول حرف من اسم مكتشفها «فراونهوفر» الألماني (خطوط فراونهوفر).
الهالة K : وهذه أيضا أشعة متشتتة على إلكترونات. ونظرا لأن سرعة حركة الإلكترونات مختلفة فإن أطوال موجات الضوء المتشتت عليها يعاني انزياح دوبلر، مما يجعل خطوط طيف فراونهوفر تنساب في طيف مستمر ولا تصبح خطوطا منفصلة واضحة.الهالة L : وهذه خطوط طيف مميزة يصدرها غاز الهالة نفسه.
========
انفجار شمسي
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
فيزياء شمسية

R C F = R P ( B s u r f 2 μ 0 ρ V S W 2 ) 1 6 {\displaystyle R_{CF}=R_{P}\left({\frac {B_{surf}^{2}}{\mu _{0}\rho V_{SW}^{2}}}\right)^{\frac {1}{6}}}
كلفة شمسية
وهج الشمس
الفروع
مجالات البحث
التجارب الحالية
العلماء
هذا الصندوق: اعرض
ناقش
عدل

صورتان متعاقبتان لظاهرة التوهج الشمسي أو التوهج الشمسي أثناء تطورها ، وقد حـُجب قرص الشمس في هاتين الصورتين لتحسين وتوضيح صورة التوهج

توهج شمسي في 31 أغسطس 2012.
الانفجار الشمسي أو التوهج الشمسي (بالإنجليزية: Solar flare)‏ هو وميض مفاجئ يزيد من سطوع الشمس، وعادةً ما يُرصد بالقرب من سطحها وعلى مقربة من مجموعات البقع الشمسية. غالبًا ما تصاحب الانبعاثات الكتلية الإكليلية الانفجارات القوية، ولكن ليس دائمًا. بالكاد يمكن رصد حتى أقوى الانفجارات ضمن الإشعاع الشمسي الكلي («الثابت الشمسي»).تحدث الانفجارات الشمسية في طيف بمقادير أسية؛ تكفي طاقةٌ مقدارها 1020 جول عادةً لإنتاج حدث يمكن رصده بوضوح، في حين أن الأحداث الكبيرة يمكن أن تطلق طاقةً تصل حتى 1025 جول.ترتبط الانفجارات الشمسية ارتباطًا وثيقًا بطرد البلازما والجسيمات من خلال هالة الشمس نحو الفضاء الخارجي؛ كما تبعث الانفجارت الشمسية موجات راديوية بكثرة. إذا كانت الانبعاثات موجهةً نحو الأرض، يمكن للجسيمات المرتبطة بها أن تخترق الغلاف الجوي العلوي (الغلاف الأيوني) وتتسبب في حدوث الشفق القطبي الساطع، وقد تعطل أيضًا الاتصالات الرادوية بعيدة المدى. عادةً ما يستغرق وصول انفجارات البلازما الشمسية إلى الأرض أيامًا.
تحدث هذه الانفجارات على النجوم الأخرى أيضًا، حيث ينطبق مصطلح الانفجارات النجمية. يمكن أن تصل الجسيمات عالية الطاقة، التي قد تكون نسبية، في نفس موعد وصول الإشعاع الكهرومغناطيسي تقريبًا.
في 23 يوليو 2012، بالكاد تفادت الأرض عاصفةً شمسيةً ضخمة (أي انفجار شمسي مع انبعاث كتلي إكليلي وإشعاع كهرومغناطيسي). في عام 2014، نشر بيت رايلي من شركة العلوم التنبؤية بحثًا حاول فيه حساب احتمال تعرض الأرض لعاصفة شمسية مماثلة خلال السنوات العشر القادمة، بمساعدة سجلات العواصف الشمسية الماضية من ستينات القرن العشرين حتى يومنا هذا. وقد توصل إلى أن احتمال حدوث ذلك هو 12%.
محتويات 1 وصف الانفجارات الشمسية
2 الأسباب
3 تصنيف الانفجارات الشمسية 3.1 تصنيف إتش ألفا
4 مخاطر الانفجارات الشمسية
5 انظر أيضًا
6 مراجع
وصف الانفجارات الشمسية
تؤثر الانفجارات الشمسية على جميع طبقات الغلاف الشمسي (الغلاف الضوئي والغلاف اللوني والهالة). يُسخن الوسط البلازمي لتصل حرارته إلى عشرات ملايين كلفن، بينما تُسرع الإلكترونات والبروتونات والأيونات الثقيلة إلى سرعة الضوء تقريبًا. تنتج الانفجارات الشمسية إشعاعًا كهرومغناطيسيًا بجميع الأطوال الموجية عبر الطيف الكهرومغناطيسي، بدءًا من الموجات الراديوية إلى أشعة جاما. تتوزع معظم الطاقة على ترددات خارج الطيف المرئي وبالتالي فإن غالبية الانفجارات غير مرئية للعين المجردة ويجب رصدها باستعمال أدوات خاصة. تحدث الانفجارات الشمسية في المناطق النشطة حول البقع الشمسية، حيث تخترق الحقول المغناطيسية الشديدة الغلاف الضوئي لتربط الهالة بالجزء الداخلي للشمس. تنبع طاقة الانفجارات الشمسية من الإطلاق المفاجئ (خلال دقائق إلى عشرات الدقائق) للطاقة المغناطيسية المُخزنة في الهالة. قد ينتج هذا الإطلاق انبعاثات كتلة إكليلية (سي إم إي)، على الرغم من أن العلاقة بين سي إم بي والانفجارات الشمسية لا تزال غير مفهومةً جيدًا.
يمكن أن تؤثر الأشعة السينية والأشعة فوق البنفسجية المنبعثة من الانفجارات الشمسية على الغلاف الأيوني للأرض ويمكن أن تعطل الاتصالات الرادوية بعيدة المدى. قد يؤدي الانبعاثات الراديوية المباشرة ذات الأطوال الموجية العشرية إلى تشويش عمل الرادارات والأجهزة الأخرى التي تستخدم هذه الترددات.
رُصدت الانفجارات الشمسية لأول مرة على الشمس من قبل ريتشارد كريستوفر كارينجتون وبشكل مستقل من قبل ريتشارد هودجسون في عام 1859
على شكل توهجات مرئية موضعية في مناطق صغيرة داخل مجموعة من البقع الشمسية. يمكن الاستدلال على الانفجارات النجمية من خلال رصد المنحنيات الضوئية في بيانات التلسكوبات أو الأقمار الصناعية لمجموعة متنوعة من النجوم الأخرى.
يختلف تواتر حدوث الانفجارات الشمسية، من عدة مرات في اليوم عندما تكون الشمس «نشطة» بشكل خاص إلى أقل من انفجار واحد كل أسبوع عندما تكون الشمس «خاملة»، على مدى الدورة الشمسية التي تستمر لـ 11 عامًا. الانفجرات الكبيرة أقل تكرارًا من الانفجارات الأصغر.
الأسبابتحدث الانفجارت الشمسية عندما تتفاعل الجسيمات المشحونة، الإلكترونات بشكل أساسي، مع الوسط البلازمي. تشير الدلائل إلى أن ظاهرة إعادة الاتصال المغناطيسي تؤدي إلى تسارع جسيمات المشحونة بقوة. على الشمس، قد تحدث إعادة الاتصال المغناطيسي في الممرات الشمسية - سلسلة من الحلقات التي تمتد على خطوط القوة المغناطيسية. تتصل خطوط القوة هذه بسرعة مع ممر سفلي من الحلقات تاركةً مجالًا مغناطيسيًا حلزونيًا غير متصل ببقية الممرات. إن الإطلاق المفاجئ للطاقة في إعادة الاتصال ما يسارع الجسيمات. قد يمتد المجال المغناطيسي الحلزوني غير المتصل والمواد التي يحتويها بعنف إلى الخارج لتشكيل انبعاثات كتلية إكليلي.
يفسر هذا أيضًا سبب اندلاع الانفجارات الشمسية من المناطق النشطة على الشمس حيث تكون المجالات المغناطيسية أقوى بكثير.
على الرغم من وجود اتفاق عام حول مصدر طاقة الانفجارات الشمسية، إلا أن الآليات المعنية لا تزال غير مفهومةً جيدًا. ليس من الواضح كيف تُحول الطاقة المغناطيسية إلى طاقة حركية تحملها الجسيمات، ومن غير المعروف كيف تُسرع بعض الجسيمات إلى نطاق طاقات جيجا إلكترون فولت (109 إلكترون فولت) وأكثر. هناك أيضًا بعض التناقضات فيما يتعلق بالعدد الإجمالي للجسيمات المتسارعة، الذي يبدو أحيانًا أكبر من العدد الإجمالي في الحلقة الإكليلية. لا يتسطيع العلماء التنبؤ بموعد حدوث الانفجارات الشمسية.
تصنيف الانفجارات الشمسية
يستخدم نظام تصنيف الانفجارات الشمسية الحروف إيه وبي وسي وإم وإكس، وفقًا لذروة التدفق، مُقاسةً بوحدة الواط لكل متر مربع (W/m2)، للأشعة السينية التي تتمتع بأطوال موجية تتراوح بين 100 و800 بيكومتر (1 و8 أنغستروم) وفقًا لقياسات قمر الرصد البيئي العامل ذو المدار الثابت (جي أوه إي إس).
يُشار إلى قوة حدث الانفجار الشمسي في كل تصنيف بعدد يتراوح بين 1 و9، والذي هو أيضًا عامل القوة للحدث داخل كل تصنيف. بالتالي، فإن انفجارًا بتصنيف إكس 2 هو أقوى بمرتين من انفجار بتصنيف إكس 1، كما أن انفجار بتصنيف إكس 3 هو أقوى بثلاث مرات من انفجار إكس 1، وأقوى بنسبة 50% فقط من إكس 2 الذي هو أقوى بأربع مرات من انفجار إم 5.
تصنيف إتش ألفا
استند تصنيف الانفجارات المبكر على عمليات رصد خط إتش ألفا الطيفي. يستند المخطط على الشدة وسطح الانبعاث. تُصنف الشدة نوعيًا، ويشير التصنيف إلى الانفجارات كما يلي: باهت (إف) أو عادي (إس) أو ساطع (بي). يُقاس سطح الانبعاث بأجزاء من المليون من نصف الكرة الشمسية. (المساحة الكلية لنصف الكرة الشمسية AH = 15.5*1012 كيلومتر مربع.)
تُصنف الانفجارات الشمسية بعد ذلك باستعمال الحرف إس أو رقم يمثل حجمها بالإضافة إلى حرف آخر يمثل ذروة شدتها، على سبيل المثال: إس إن هو انفجار شمسي عادي.
مخاطر الانفجارات الشمسية
تؤثر الانفجارات الشمسية بقوة على الطقس الفضائي القريب من الأرض. يمكنها إنتاج تيارات من الجسيمات عالية الطاقة في الرياح الشمسية أو الرياح النجمية، المعروفة باسم حدث البروتون الشمسي. يمكن أن تؤثر هذه الجسيمات على الغلاف المغناطيسي للأرض، وقد تمثل خطرًا إشعاعيًا للمركبات الفضائية ورواد الفضاء. بالإضافة إلى ذلك، تصاحب الانبعاثات الكتلية الإكليلية (سي إم إي) الانفجارات الشمسية الضخمة في بعض الأحيان، التي يمكن أن تؤدي إلى عواصف جيومغناطيسية التي أدت في السابق إلى تعطيل الأقمار الصناعية وشبكات الطاقة الكهربائية الأرضية لفترات طويلة.
يزيد تدفق الأشعة السينية الضعيفة، لانفجارات الفئة إكس، التأين في الغلاف الجوي العلوي، الذي يمكن أن يتداخل مع الاتصالات الرادوية القصيرة ويمكن أن يسخن الغلاف الجوي الخارجي ليزيد تاثير المقاومة الهوائية على الأقمار الصناعية في المدارات المنخفضة، وبالتالي تدهور هذه المدارات. تساهم الجسيمات النشطة في الغلاف المغناطيسي بتكوين الشفق القطبي الشمالي والجنوبي. يمكن أن تسبب طاقة الأشعة السينية القوية ضررًا بإلكترونيات المركبات الفضائية، وعادةً ما تنتج عن انبعاثات البلازما الضخمة في الغلاف اللوني العلوي للشمس.
تمثل مخاطر إشعاعات الانفجارات الشمسية مصدر قلق كبير في مناقشة المهمات المأهولة إلى المريخ أو القمر أو الكواكب الأخرى. يمكن للبروتونات النشطة أن تمر عبر جسم الإنسان، ما يسبب تلفًا كيميائيًا حيويًا لرواد الفضاء أثناء السفر بين الكواكب. من الضروري وجود نوع من الحماية المادية أو المغناطيسية لرواد الفضاء. تستغرق معظم العواصف البروتونية ساعتين على الأقل من وقت الكشف البصري قبل وصولها إلى مدار الأرض. أطلق انفجار شمسي حدث في 20 يناير 2005 أعلى تركيز من البروتونات تم قياسه مباشرةً على الإطلاق،
ما منح رواد الفضاء 15 دقيقة فقط للوصول إلى المأوى للحماية.
===
فيض راديوي شمسي
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
الفيض الراديوي الشمسي أو فيض الأشعة الراديوية الشمسي (بالإنجليزية:Solar Radio Flux) هو أشعة شمسية في حيز الموجات الراديوية ولها طول موجة قدرها 7و10 سنتيمتر، أي ذات تردد 2800 ميجا هرتز. تسمى تلك الأشعة أيضا فيض 7و10 سنتيمتر أو «مؤشر كوفينجتون» لفيض الشمس.

متوسط الفيض الراديوي الشمسي شهريا بقمته العظمى ونهايته الصغرى بين 1994 - 2010.

دورات النشاط الشمسي 21, 22 and 23 ممثلة بمؤشر عدد البقع الشمسية (أزرق), و الفيض الراديوي 10.7 سنتيمتر (بنفسجي) , وكذلك مؤشر الانفجارات الشمسية (أخضر).

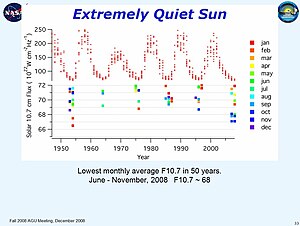
النهايات الصغرى الشهرية للفيض الراديوي الشمسي منذ 1950 .
محتويات 1 أهميته
2 تطبيقاته
3 المراجع
4 اقرأ أيضا
أهميته
يتناسب مؤشر الفيض الراديوي الشمسي تناسبا طرديا مع النشاط الشمسي.وهو يعتمد في نفس الوقت على عدد البقع الشمسية، ولكن من السهل قياسه عن رصد عدد البقع الشمسية. وقد اكتشف «آرثر كوفينجتون» هذه العلاقة بين عدد البقع الشمسية ومؤشر الفيض الراديوي في عام 1946 أثناء دراسته لخسوف الشمس وتأكد من افتراضه.
تقاس شدة الإشعاع بوحدة [واط/متر مربع/هرتز ] ، وتسمى تلك الوحدة أيضا جانسكي أو «وحدة فيض الشمس» (sfu):1 sfu = 104 Jy = 10−22 W m−2 Hz−1
تقوم مراصد كثير في البلاد المختلفة بقياس الفيض يوميا من على سطح الأرض. وهو يصلح لتعيين النشاط الشمسي بطريقة أحسن من طريقة رصد عدد البقع الشمسية وأكثر دقة. .
تطبيقاته
يستخدم مؤشر الفيض الراديوي للشمس في للتنبؤ بالأحوال الجوية المناسبة للاتصالات في نطاق الموجات اللاسلكية القصيرة، حيث أن درجة تأين طبقة أيونوسفير المسؤولة عن انعكاس الموجات القصيرة إلى الأرض يعتمد مباشرة على النشاط الشمسي. ولكن الإشعاع الراديوي الشمسي بطول موجته البالغة 7و10 سنتيمتر لا تكون قادرة على تأين طبقة الأيونوسفير، وإنما تقوم بذلك ما يرافقها من أشعة فوق البنفسجية وأشعة إكس من الشمس. ولهذا يؤخذ ما تقيسه الأقمار الصناعية لفيض أشعة إكس كمقياس لدرجة تأين طبقة الأيونوسفير في جو الأرض.
استخدام آخر وهو يستغل طبيعة انكسار الفيض الراديوي الشمسي وانتقاله على حافة الشمس . فهو يسمح بذلك بمعرفة ما يجري من نشاط على الوجه الآخر من الشمس حيث ينعكس الفيض على حافة الشمس فنراه.
=========
عنقود مجرات العذراء العظيم
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
{{{الاسم}}}

بيانات المراقبة
الكوكبات العذراء

شاهد ايضا: تجمع مجري, العنقود المجري, قائمة مجموعات وعناقيد المجرات
تعديل مصدري - تعديل

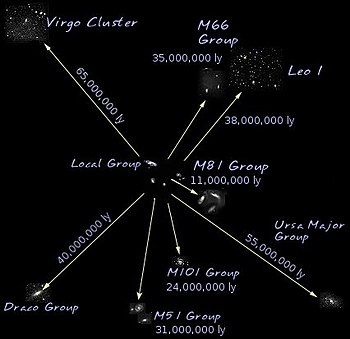
المسافات بيننا (المجموعة المحلية) و بعض تجمعات المجرات حولنا. إلى أعلى اليسار تجمع مجرات العذراء.
عنقود مجرات العذراء العظيم (بالإنجليزية: Virgo Supercluster أو Local Supercluster) هو تجمع مجري هائل غير منتظم يتكون من تجمع مجرات العذراء بالإضافة إلى المجموعة المحلية التي توجد فيها مجرة درب التبانة و المجرة الكبيرة المرأة المسلسلة. يوجد في هذا العنقود العظيم 100 مجموعة مجرات على الأقل، في حجم يبلغ قطره نحو 33 مليون فرسخ فلكي، أي نحو 110 مليون سنة ضوئية. يشكل هذا العنقود العظيم واحدا من نحو مليون من أمثاله من العناقيد المجرية العظيمة الموجودة في الكون المرئي.
محتويات 1 مقدمة
2 تجمعات مجرات وتجمعات نجوم فيها
3 عنقود مجرات العذراء العظيم وتكوينه في الكون
4 المراجع
5 وصلات خارجية
6 اقرأ أيضا
مقدمة

جيران عنقود العذراء العظيم من العناقيد العظيمة الأخرى و فراغات (فلك) و خيوط مجرات .

موقع عنقود مجرات العذراء العظيم (إلى اليمين و أعلى اليمين) بالنسبة إلى المجموعة المحلية Local group . إلى أسفل اليسار يـُرى مجموعة مجرات الكور Fornaux group .
يحوي عنقود مجرات العذراء العظيم بين 100 إلى 200 مجموعة مجرات. ويتمركز في وسطه تجمع مجرات العذراء المتكون من نحو 2000 مجرة ، ولهذا فقد سمي العنقود العظيم باسمه. مثل تلك التجمعات المجرية نجد مجموعة مجرات الكور و مجموعة مجرات النهر. توجد مجموعتنا المحلية من المجرات ومجموعات أخرى مثل مجموعة مجرات م81 و مجموعة مجرات م83 و مجموعة مجرات النحات في الوسط تقريبا بين مجموعة مجرات الكور ومجموعة مجرات العذراء.
يبلغ قطر حجم عنقود مجرات العذراء العظيم نحو 150 إلى 200 مليون سنة ضوئية، وهو في شكل القرص.
وتبلغ الكتلة الكلية لهذا العنقود العظيم ربما ما يزيد عن 1015 كتلة شمسية (أي نحو 2 × 1045 كيلوجرام). وقد توصل العلماء إلى هذا التقدير عن طريق رصد تأثيرات الجاذبية التي تعمل على تحريك المجرات . ونظرا لأن شدة ضياء عنقود العذراء العظيم تهتبر منخفضة بمقارنتها بعدد النجوم فيها فإن ذلك يشير إلى حتمية وجود ما يسمى مادة مظلمة . ويعتقد العلماء أن المادة المظلمة تكون الجزء الأكبر من الكتلة في عنقود العذراء العظيم .
يتحرك عنقود مجرات العذراء العظيم في اتجاه عنقود هيدرا قنطورس العظيم بسرعة تبلغ نحو 600 كيلومتر /الثانية - بالإضافة إلى عدة عناقيد مجرات عظيمة أخرى - في اتجاه وبنفس السرعة في اتجاه تشكيل أعظم أكتشف عام 1990 يسمى الجاذب العظيم ، وهو يبعد عنا نحو 200 مليون سنة ضوئية.
تجمعات مجرات وتجمعات نجوم فيها
الصورة المعتادة التي يحصل عليها الفلكيون عن رصد مناطق الكون المختلفة هي أن المجرات تتركز في تجمعات منها وعناقيد ، تربط بينها خيوط أو فتائل مكونة من مجرات كما تفصلها في نفس الوقت فراغات كونية بالغة الكبر لا يوجد بها مجرات تصل مقاييس تلك الفاراغات إلى 200 -400 مليون سنة ضوئية ويصبح الشكل العام شكلا عنكبوتيا . وأينما قام الفلكيوين بتوجيه تلسكوباتهم في أنحاء الكون المختلفة يجدوا هذا الشكل العام ، أي لا يتميز اتجاه عن اتجاه ولا ركن من أركان الكون عن الآخر . هذا بصرف النظر عن أنه كلما كانت الصورة قادمة من ركن بعيد في الكون كانت صورته لدينا تنتمي إلى وقت سحيق سابق . نظرا لأن الضوء القادم من مجرات بعيدة يأتي إلينا بسرعة الضوء البالغة نحو 300 ألف كيلومتر في الثانية فغن الصورة التي نراها حاليا هي هيئته التي كان عليها عندما غادره الضوء . أي أنه كلما كنا ننظر إلى أماكن بعيدة في الكون كنا نري الماضي.
عنقود مجرات العذراء العظيم هو أحد التجمعات الهائلة للمجرات، وهو يتصف بمجموعات المجرات وتجمعات النجوم التالية:
الاسم البعد عن
المجموعة المحلية
(مليون سنة ضوئية)
المجموعة المحلية —
مجموعة مجرات مافاي 6–12
مجموعة مجرات النحات 10
مجموعة مجرات م81 10–11
مجموعة مجرات م83 (أو NGC 5128 Group) 12–17
مجموعة مجرات السلوقيان 1 (أو مجموعة مجرات م94 ) 13–18>(مسييه 94)>
NGC-4631مجموعة مجرات 25
مجموعة مجرات مسييه 96 35 (مسييه 96)
مجموعة مجرات دورادو 48–60 (إن جي سي 1553 / NGC 1566)
مجموعة مجرات الكور 60
تجمع مجرات العذراء 65
مجموعة مجرات الأسد 2 70 (NGC 3607)
مجموعة مجرات الدب الأكبر 75
مجموعة مجرات العذراء 3 65–82 (NGC 5569 / NGC 5713)
مجموعة مجرات النهر 69–100 (إن جي سي 1300 / إن جي سي 1232)
عنقود مجرات العذراء العظيم وتكوينه في الكون

صور توضح موقعنا في الكون المرئي. Click here for larger image ، الصور من اليسار إلى اليمين :1) الأرض ، 2) المجموعة الشمسية ، 3) جيران المجموعة الشمسية ، 4) مجرتنا ، 5 )مجموعة المجرات المحلية ، 7) عنقود مجرات العذراء العظيم ، 8) الكون .
======
هيدروديناميكا مغناطيسية
من ويكيبيديا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
هيدروديناميكا مغناطيسية
صنف فرعي من
ميكانيكا الموائع
جزء من
hydrodynamics (en)
تعديل - تعديل مصدري - تعديل ويكي بيانات

الشمس هي محطة توليد هيدروديناميكية مغناطيسية لم تُدرس بشكل جيد حتّى الآن
علم الهيدروديناميكية المغناطيسيّة ويسمى أيضاً (علم ديناميكية أوهيدروليكية السوائل المغناطيسية) هو العلم الذي يدرس الخصائص المغناطيسية وسلوك الموائع الموصلة كهربائيّاً. ومن أمثلة الموائع المغناطيسية (البلازما، المعادن السائلة، المياه الملحية، المحاليل الكهربائيّة والإلكتروليتات).
كلمة الهيدروديناميكيّة المغناطيسيّة أو " Magnetohydrodynamics" مشتقة من (Magneto) وتعني الحقل المغناطيسي، (Hydro) وتعني المياه، و (Dynamic)وتعني الحركة. علم الهيدروديناميكية المغناطيسيّة أو ما يعرف اختصاراً بـ (MHD) أُسِّسَ على يد العالم السويدي هانز ألفين الذي حصل على جائزة نوبل في الفيزياء في عام 1970 وذلك لتأسيسه لهذا العلم.
المفهوم الأساسي للـ MHD هو أنّ المجالات المغناطيسية يمكن أن تحفّز التيارات في المائع المتحرك الذي يحمل خاصية الموصليّة الكهربائية، مما يؤدّي لاستقطاب المائع وتغيير المجال المغناطيسي له بالتبادل. إنّ مجموعة المعادلات التي تصف (MHD) هي مزيج من معادلات نافييه-ستوكس لديناميكا الموائع ومعادلات ماكسويل للكهرومغناطيسية. يجب حل هذه المعادلات التفاضلية المترابطة، إما تحليليًا أو عدديًا.
محتويات 1 تاريخ الـ (الهيدروديناكيكية المغناطيسية)
2 الهيدروديناكيكية المغناطيسية المثالية والمقاومة 2.1 معادلات MHD المثالية
2.2 قابلية تطبيق الـ MHD المثالي على البلازما
2.3 أهمية المقاومة
2.4 أهمية التأثيرات الحركية
3 البنية في أنظمة الهيدروديناكيكية المغناطيسية
4 اقرأ أيضا
5 المصادر
تاريخ الـ (الهيدروديناكيكية المغناطيسية)أول استخدام مسجل لمصطلح (الهيدروديناكيكية المغناطيسية) تمّ من قبل العالم والمهندس الكهربائي السويدي هانز ألففين عام 1942 عندما قال: «أخيرًا، بعض الملاحظات حول نقل النشاط من الشمس إلى الكواكب، وهو أمر أساسي للنظرية (§11). وأشير إلى أهمية الموجات الهدروديناميكية المغناطيسية في هذا الصدد.»المياه المالحة المنحسرة المتدفقة عبر جسر ووترلو في لندن تتفاعل مع الحقل المغناطيسي الأرضي مخلّفة فرق في الكمون ما بين ضفتي النهر. وصف مايكل فاراداي هذا التأثير بأنه «تحريض كهرطيسي» وقام بهذه التجربة عام 1832 لكن التيار الذي نتج عنها كان صغيراً جدّاً بحيث لا يمكن قياسه بالمعدّات الموجودة في ذلك الزمن، وقد ساهم قاع النهر في قصر الإشارة الكهربائية الناتجة. ومع ذلك، فقد تمّ قياس الجهد الناجم عن حركات المد والجزر في القنال الإنجليزي عام 1851من خلال عملية مشابهة.
الهيدروديناكيكية المغناطيسية المثالية والمقاومة
إنّ أبسط أشكال الهيدروديناميكية المغناطيسة هي الهيدروديناميكية المغناطيسية المثالية (Ideal MHD)، يُفترض في هذه الحالة أنّ السائل لديه مقاومة قليلة جدّاً لدرجة أنه يمكن التعامل معه على أنّه موصل مثالي. وهذه الحالة نكون عند الحد الأعلى لعدد رينولد المغناطيسي.
في الـ MHD المثالي، يَفرِضُ قانون لينز أنّ السائل مرتبط إلى حدٍّ ما بخطوط المجال المغناطيسي. للتوضيح، فإنّ في حالة الـ MHD المثالي، يأخذ حجمٌ صغيرٌ من السوائل شكل حبل يحيط بخط الحقل ويتوضع على طول خط المجال المغناطيسي، حتّى عندما يكون ملتويًا ومشوَّهًا بتدفّقات السوائل في النظام. ويشار إلى ذلك أحياناً باسم)خطوط المجال المغناطيسي «المجمدة» في السائل). [5] العلاقة بين خطوط الحقل المغنطيسي والسوائل في الـ MHD المثالي تعمل على إصلاح طوبولوجيا المجال المغناطيسي في السائل - على سبيل المثال، إذا رُبطت مجموعة من خطوط المجال المغناطيسي لتُشَكّل عقدة، فستبقى هكذا طالما أن السائل أو البلازما لديه مقاومة قليلة جدّاً لدرجة يمكن إهمالها. هذه الصعوبة في إعادة ربط خطوط الحقل المغناطيسي تجعل من الممكن تخزين الطاقة عن طريق تحريك السائل أو مصدر المجال المغناطيسي. ومن الممكن أن تصبح الطاقة متاحة إذا لم تعد حالة الـ MHD مثالية، مما يسمح بإعادة الاتصال المغناطيسي وهو ما يحرر الطاقة المخزنة من المجال المغناطيسي.
معادلات MHD المثالية
تتكون معادلات الـ MHD المثالية من: معادلة الاستمرارية، معادلة كوشي للقوّة الدافعة، قانون أمبير مع إهمال تيّار الإزاحة، ومعادلة تطور الحرارة. كما هو الحال مع أيّ وصف لأيّ سائل بأي نظام ناشط، يجب تطبيق مقاربة الإغلاق عند أعلى عزم في معادلة توزيع الجسيمات. يتم تحقيق هذا في أغلب الأحيان بالتقريب إلى تدفق الحرارة بعملية إيزوثيرميّة (أي بثبات درجة الحرارة) أو بعملية أديباتيّة (أي في بيئة معزولة عن الوسط الخارجي بحيث لا يحدث تبادل حراري بين الوسط الذي تحدث فيه العملية والوسط الخارجي)
إن المعايير الرئيسية التي تميّز السائل الموصل كهربائياً هي: حقل سرعة البلازما السائلة v ، وكثافة التيار J ، والكثافة الكلية ρ، وضغط البلازما p. إنّ الشحنة الكهربائية المتدفّقة في البلازما هي مصدر المجال المغناطيسي B والحقل الكهربائي E. بشكل عامّ فإن جميع المعايير السابقة تتفاوت مع الزمن t. يُستخدم عادةً رمز المتّجه في هذه المعادلات، بالتفصيل: (الرمز ودلالته): ∇: يرمز للتدرج، ∇⋅: يرمز للتباعد، و ∇ ×: يرمز للتموج.
معادلة استمرارية الكتلة هي: ∂ ρ ∂ t + ∇ ⋅ ( ρ v ) = 0. {\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot \left(\rho \mathbf {v} \right)=0.}
معادلة كوشي للقوّة الدافعة هي: ρ ( ∂ ∂ t + v ⋅ ∇ ) v = J × B − ∇ p . {\displaystyle \rho \left({\frac {\partial }{\partial t}}+\mathbf {v} \cdot \nabla \right)\mathbf {v} =\mathbf {J} \times \mathbf {B} -\nabla p.}
يمكن توسيع مصطلح قوة لورينتز J × B باستخدام قانون أمبير والمحددات الخاصة بمتجه الحركة 1 2 ∇ ( B ⋅ B ) = ( B ⋅ ∇ ) B + B × ( ∇ × B ) {\displaystyle {\frac {1}{2}}\nabla (\mathbf {B} \cdot \mathbf {B} )=(\mathbf {B} \cdot \nabla )\mathbf {B} +\mathbf {B} \times (\nabla \times \mathbf {B} )}
ما يعطي: J × B = ( B ⋅ ∇ ) B μ 0 − ∇ ( B 2 2 μ 0 ) , {\displaystyle \mathbf {J} \times \mathbf {B} ={\frac {\left(\mathbf {B} \cdot \nabla \right)\mathbf {B} }{\mu _{0}}}-\nabla \left({\frac {B^{2}}{2\mu _{0}}}\right),}
حيث: الطرف الأوّل هو قوّة الشد المغناطيسي والطرف الثاني يمثّل قوّة الضغط المغناطيسيّة ويتمّ إعطاء قانون أوم المثالي للبلازما بالشكل التالي: E + v × B = 0. {\displaystyle \mathbf {E} +\mathbf {v} \times \mathbf {B} =0.}
وقانون فاراداي هو: ∂ B ∂ t = − ∇ × E . {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}=-\nabla \times \mathbf {E} .}
يهمل قانون أمبير منخفض التردّد تيار الإزاحة ويعطى بالعلاقة: μ 0 J = ∇ × B . {\displaystyle \mu _{0}\mathbf {J} =\nabla \times \mathbf {B} .}
علاقة التباعد المغناطيسي الكابح هي: ∇ ⋅ B = 0. {\displaystyle \nabla \cdot \mathbf {B} =0.}
ومعادلة الطاقة تكون بالشكل التالي: d d t ( p ρ γ ) = 0 , {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {p}{\rho ^{\gamma }}}\right)=0,}
حيث γ = 5/3 هي نسبة درجات الحرارة المعيّنة لمعادلة ثابت الحرارة للحالة. هذه المعادلة للطاقة ولا تطبّق إلّا في حالة انعدام وجود صدمات أو توصيل للحرارة، حيث أنّ المعادلة تفترض أن الإنتروبيا لعنصر مائع لا يتغير.
قابلية تطبيق الـ MHD المثالي على البلازما
لا ينطبق MHD المثالي إلا عندما: تكون البلازما شديدة الصلابة بحيث يكون المقياس الزمني للتّصادمات أقصر من الأوقات المميًزة الأخرى في النظام، وبالتالي يكون توزيع الجسيمات قريب من توزيع (ماكسويل).
أن تكون المقاومة صغيرة بسبب هذه الاصطدامات. على وجه الخصوص، يجب أن تكون أوقات الانتشار للمغناطيسية النموذجية على طول أي مقياس موجود في النظام أطول من أي مقياس زمني.
الاهتمام بمقاييس الطول أطول بكثير من عمق القشرة الأيونيّة ونصف قطر لارمور المتعامد مع الحقل، طويل على كل مسافة الحقل بشكل يكفي لإهمال تخميد لانداو، وقياس الوقت أطول بكثير من زمن الدوران الأيوني (النظام سلس ومتطور ببطء).
أهمية المقاومة
في السائل الموصِل بشكل غير كامل، يمكن للحقل المغنطيسي أن يتحرّك خلال السائل تبعاً لقانون الانتشار وذلك مع مقاومة البلازما التي تكون بمثابة ثابت للانتشار. وهذا يعني أن حلول معادلات MHD المثالية لا تنطبق إلّا على فترة زمنية محدودة لمنطقة ذات حجم معين معطى قبل أن يصبح الانتشار كبيراً للغاية بحيث لا يمكن تجاهله. يمكن تقدير زمن الانتشار عبر منطقة نشطة بالطاقة الشمسية (من مقاومة الاصطدام) من مئات إلى آلاف السنين، أطول بكثير من العمر الفعلي للبقعة الشمسية، لذا يبدو من المعقول تجاهل المقاومة. وعلى النقيض من ذلك، فإن متر مكعب من مياه البحر يحتوي على زمن انتشار مغناطيسي يقاس بالمللي ثانية.
حتى في الأنظمة الفيزيائية - الكبيرة والموصلة بدرجة كافية، بحيث تقترح التقديرات البسيطة لرقم لاندكويست إلى أنه يمكن تجاهل المقاومة - قد تظل المقاومة مهمّة: العديد من حالات عدم الاستقرار يمكن أن تزيد من المقاومة الفعّالة للبلازما من خلال عدة عوامل ما يزيد عن مليار مرّة. تتكوّن المقاومة المعزّزة عادة نتيجة لتشكيل بنية صغيرة الحجم مثل تيار الصفائح أو الاضطراب المغناطيسي الرقيق النطاق، بإدخال مقاييس مكانية صغيرة في النظام الذي يتم فيه كسر الـ MHD المثاليّ يمكن أن يحدث الانتشار المغناطيسي بسرعة. عند حدوث ذلك، قد يحدث إعادة اتصال مغناطيسي في البلازما لتحرير الطاقة المغناطيسية المخزنة كموجات، وتسارع ميكانيكي كبير للمواد، وتسارع الجسيمات، والحرارة.
إنّ إعادة الربط المغنطيسي في الأنظمة عالية التوصيل أمر مهم لأنّه يركز الطاقة في الزمان والمكان، بحيث يمكن للقوى الصغيرة المطبّقة على البلازما لفترات طويلة من الزمن أن تتسبّب في حدوث انفجارات عنيفة وانبعاثات إشعاعيّة.
عندما لا يمكن اعتبار السوائل موصلة بالكامل، مع تحقّق الشروط الأخرى للـ MHD المثالي بشكل مرضٍ، فمن الممكن استخدام نموذج موسّع يسمى (MHD مقاوم). وهذا يشمل مصطلح إضافي في قانون أوم الذي يميّز المقاومة الاصطلاحية. بشكل عام، تكون المحاكاة الحاسوبية لـ MHD مقاومة بعض الشيء، نظرًا لأن شبكتها الحاسوبية تُدخل مقاومة رقمية.
أهمية التأثيرات الحركية
هناك قيد آخر لـ MHD (ونظريات السوائل بشكل عام) هو أنّها تعتمد على افتراض أن البلازما هي شديدة الاصطدام (وهذا هو المعيار الأول المذكور أعلاه)، بحيث يكون المقياس الزمني للتصادمات أقصر من الأوقات المميزة الأخرى في النظام، وتوزيعات الجسيمات تكون بطريقة ماكسويل. وهذا ليس هو الحال عادة في البلازما الاندماجية والفضائية والفيزياء الفلكية. وعندما لا يكون هذا هو الحال، أو عندما تكون الدراسة في المقاييس المكانية الأصغر، قد يكون من الضروري استخدام نموذج حركي يقوم بالحسابات لعامل التوزيع للشكل غير الماكسويلي بشكل صحيح. ومع ذلك، نظرًا لأن MHD بسيط نسبيًا ويلتقط العديد من الخصائص المهمة لديناميكيات البلازما، فغالبًا ما يكون دقيقًا بشكلٍ نوعيّ، ولذلك غالبًا ما يكون النموذج الأول للتجارب.
التأثيرات الحركية بشكل أساسي والتي لا يتم التقاطها بواسطة النماذج السائلة تشمل تشكّل طبقات مزدوجة، تخميد لانداو، مجموعة واسعة غير مستقرة، الفصل الكيميائي في البلازما الفضائية والإلكترون الجامح. في حالة تفاعلات الليزر فائقة الكثافة، تعني الجداول الزمنية القصيرة للغاية لترسب الطاقة أن الرموز الهيدروديناميكية تفشل في تفسير الفيزياء الأساسية.
البنية في أنظمة الهيدروديناكيكية المغناطيسية
في العديد من أنظمة MHD ، يتم ضغط معظم التيار الكهربائي إلى أشرطة رقيقة شبه ثنائية الأبعاد تسمّى صفائح التيار. من الممكن أن تقسم هذه الصفائح السائل إلى عدّة مجالات مغناطيسية، والتي تكون فيها التيّارات ضعيفة نسبيّاً. ويُعتقد أنّ صفائح التيار في الهالة الشمسيّة تتراوح بين بضعة أمتار وبضعة كيلومترات في السماكة، وهي رقيقة إلى حد ما مقارنة بالمجالات المغناطيسية (التي تتراوح بين آلاف ومئات الآلاف من الكيلومترات). وهناك مثال آخر في الغلاف المغناطيسي للأرض، حيث تفصل صفائح التيار مجالات مميزة من الناحية الطوبولوجية، مما يعزل معظم الغلاف الجوي للأرض عن الرياح الشمسية.
وتسمى صيغ الموجة المشتقّة باستخدام نظرية MHD البلازما بموجات المغناطيسية الهيدروديناميكية أو موجات MHD. بشكل عام هناك ثلاثة أنماط لموجة MHD: موجة إلفين الخالصة (أو المائلة)
موجة MHD بطيئة
موجة MHD سريعة
كل الموجات السابقة لها سرعات طور ثابتة عند جميع الترددات وبالتالي لا يوجد أي تشتّت. وعند الحدود أي عندما تكون الزاوية بين متجه انتشار الموجة k والحقل المغنطيسي B إما (0) (180) أو (90) درجة، تُسمّى أوضاع الموجة.
سرعة المرحلة تتعلق بشكل مباشر بالزاوية بين شعاع الموجة المغناطيسية K والحقل المغناطيسي B، تنتشر موجة الـ MHD في زاوية عشوائية وتتعلق بالوقت وتراكم الحقل وحجمه B0 الذي يعوض تشتت الرابطة
ω k = v A cos ⁡ θ {\displaystyle {\frac {\omega }{k}}=v_{A}\cos \theta } حيث
v A = B 0 μ 0 ρ {\displaystyle v_{A}={\frac {B_{0}}{\sqrt {\mu _{0}\rho }}}} هي سرعة إلفين، هذا الفرع يتوافق مع موجة إلفين القاصة. بالإضافة إلى ذلك تعطي معادلة التشتت العلاقة التالية:
ω k = [ 1 2 ( v A 2 + v s 2 ) ± 1 2 ( v A 2 + v s 2 ) 2 − 4 v s 2 v A 2 cos 2 ⁡ θ ] 1 2 {\displaystyle {\frac {\omega }{k}}=\left[{\frac {1}{2}}(v_{A}^{2}+v_{s}^{2})\pm {\frac {1}{2}}{\sqrt {(v_{A}^{2}+v_{s}^{2})^{2}-4v_{s}^{2}v_{A}^{2}\cos ^{2}\theta }}\right]^{\frac {1}{2}}} حيث
v s = γ p ρ {\displaystyle v_{s}={\sqrt {\frac {\gamma p}{\rho }}}}
هي سرعة الصوت في الغاز المثالي. يتوافق فرع إشارة الموجب في المعادلة مع نمط موجة MHD السريعة بينما يتوافق الفرع ذو إشارة السالب في المعادلة مع وضع الموجة البطيئة MHD. سوف يتم تثبيط ذبذبات MHD إذا لم يكن السائل موصلا بشكل كامل إنّما موصليته محدودة، أو إذا كانت هناك تأثيرات لزجة.
تعتبر الموجات والتذبذبات MHD أداة شائعة للتشخيص عن بعد للبلازما المعملية والفيزياء الفلكية، على سبيل المثال. الهالة من الشمس (علم الزلازل الاكليلي). ستتثبّط ذبذبات الـ MHD إذا كان السائل ذو صلية محدودة وليس بشكل كامل، أو إذا تعرّض لعوامل لزجة.
تعتبر موجات وتذبذبات الـ MHD أداة شائعة للتشخيص عن بعد للبلازما المخبرية وبلازما الفيزياء الفلكية، على سبيل كمثال: هالة الشمس (علم الاهتزازات في الهالة الشمسية).
علاقة سرعة المرحلة مع الزاوية Θ في حالتين: الأولى VA > VS
اقرأ أيضاشمس
نجم
اندماج نووي
مجرة
كلف الشمس
استشعار عن بعد
مسبار فضائي
مقراب جيمس ويب الفضائي
مرصد كيك
مقراب سبيتزر الفضائي
مرصد هابل الفضائي
الكيمياء الكهرومغناطيسية.
================